Пусть АО - перпендикуляр к плоскости α. Значит АО - искомое расстояние.
Тогда ВО и СО - проекции наклонных АВ и АС на плоскость.
19 > 2√70, а большей наклонной соответствует большая проекция, если наклонные проведены из одной точки.
Пусть х - коэффициент пропорциональности, тогда ОС = 5х, ОВ = 4х.
Из прямоугольных треугольников АОВ и АОС выразим АО по теореме Пифагора:
АО² = АВ² - ВО² = 280 - 16х²
АО² = АС² - СО² = 361 - 25х²
280 - 16x² = 361 - 25x²
9x² = 81
x² = 9
x = 3 (x = - 3 не подходит по смыслу задачи)
АО² = 280 - 16 · 3² = 280 - 144 = 136
АО = √136 = 2√34 см
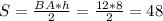
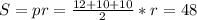
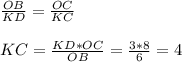
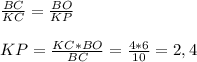
не понял, зачем публиковать 2 раз уже решенную задачу
Хорды BD и DC равны.
теорема косинусов для BD и DC (из треугольников ABD и ADC)
Пусть BD = DC= а, и еще я обозначу ПОЛОВИННЫЙ угол DAB = угол DAC = Ф;
а^2 = 1^2 + 6^2 - 2*1*6*cos(Ф);
a^2 = 8^2 + 6^2 - 2*8*6*cos(Ф);
Приравниваем, получаем cos(Ф) = 3/4;
sin(Ф) = корень(1 - 9/16) = корень(7)/4;
Вычисляем
а^2 = 1 + 36 - 2*1*6*(3/4) = 28; a = 2*корень(7);
и по теореме синусов R = a/(2*sin(Ф));
R = 4.