a) 10.
Объяснение:
Поскольку варианты ответов - скалярные величины, читаем вопрос условия так: " Найти скалярное произведение векторов АВ и EF".
Отметим координаты точек в соответствии с данным рисунком:
A(3;0;0), B(0;2;4), C(0;5;4) и D(3;7;0). Тогда координаты точек Е и F найдем, как координаты середин отрезков АВ и CD.
Эти координаты - полусуммы соответствующих координат начала и конца отрезков, то есть
Xe = (3+0)/2 =1,5; Ye = (0+2)/2 = 1 и Ze = (0+4)/2 =2.
Xf = (0+3)/2 =1,5; Yf = (5+7)/2 = 6 и Zf = (4+0)/2 = 2.
Координаты векторов АВ и EF как разность соответствующих координат конца и начала векторов:
АВ{(0-3);(2-0);(4-0)} = {-3;2;4} и соответственно EF{0;5;0}.
Скалярное произведение векторов - это сумма произведений их соответствующих координат:
АВ*EF = -3*0 + 2*5 + 4*0 = 10.
∠ABC = 180° - 99° = 81°
∠TAB + ∠BAC = 180°, т.к. это смежные углы.
∠BAC = 180° - 134° = 46°
Сумма углов треугольника равна 180°.
∠ACB = 180° - 46° - 81° = 53°
∠ACB + ∠ECB = 180°, т.к. это смежные углы.
∠ECB = 180° - 53° = 127°
ответ Сумма внешних углов равна 360°
∠ECB = 360° - 134° - 99° = 127°
ответ т.к. это смежные углы.
∠ABC = 180° - 99° = 81°
∠TAB + ∠BAC = 180°, т.к. это смежные углы.
∠BAC = 180° - 134° = 46°
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
∠ECB = 46° + 81° = 127°
ответ: 127°.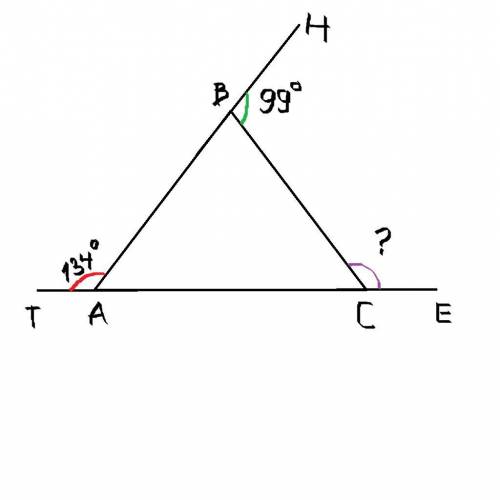
AE, BF - биссектрисы
∠AOB=90 (угол между биссектрисами внутренних углов при параллельных)
Биссектриса AO является высотой, следовательно и медианой, BO=OF.
В четырехугольнике OBCE сумма противоположных углов 180 =>
∠OBC =180-∠OEC =∠OED
OBCE=OEDF (по трем углам и двум смежным сторонам)
S(ABCE) =S(ABO)+S(OBCE) =S(AFO)+S(OEDF) =S(AED)
ED =AD tg(A/2)
S(AED) =1/2 AD^2 tg(A/2)
S(ABCD) =2 S(AED) =AD^2 tg(A/2)