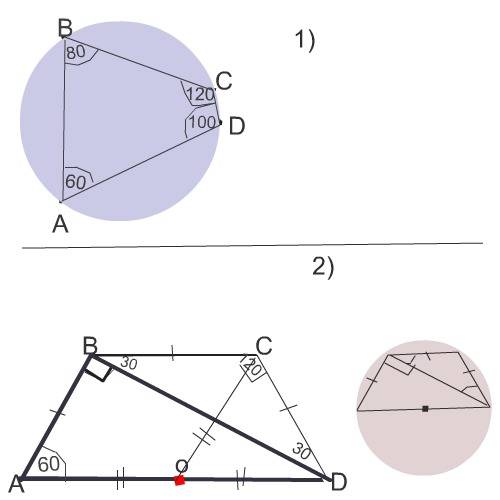
1) Поскольку этот четырехугольник вписанный, сумма его противоположных углов равна 180°
Угол D, противолежащий углу В=80, равен 100; угол С, противолежащий углу А=60, равен 120°
------------------
2)Вокруг трапеции можно описать окружность тогда и только тогда, когда ее боковые стороны равны.
Если основание и боковые стороны трапеции равны, то один из треугольников, на которые диагонали делят трапецию, равнобедренный, основанием в нём является диагональ.
Треугольник ВСD равнобедренный, углы ВDС=СВD.
Угол ВСD=180-60=120°
Отсюда угол ВDС= СDВ= (180-60):2=30°.
Углы АВD и АСD равны 120-30=90°
Следовательно, треугольники АВD и ACD - прямоугольные.
Центр описанной вокруг прямоугольного треугольника окружности лежит на середине его гипотенузы.
24°, 24°, 96°, 216°
Объяснение:
в любом четырёхугольнике сумма углов составляет 360°. обозначим эти пропорциональные числа:
9х, 4х, х, х и составим уравнение:
х+х+4х+9х=360
15х=360
х=360÷15=24
Итак: два угла в 4-хугольнике по 24°, тогда угол 4х=4×24=96°, а угол 9х=9×24=216°
Проверим: 24×2+95+216=360°