Проведём высоту ВД=АВ*cos30=4*0,866=3,46. Из точки М проведём к АС высоту МЕ. Получим два прямоугольных подобных треугольника ДВС и ЕМС(поскольку у низ по условию ВМ=МС). МЕ параллельна ВД и проходит через середину ВС следовательно это средняя линия треугольника ДВС. Отсюда МЕ=ВД/2=1,73. И ДЕ=ЕС. Косинус угла АМЕ равен cos аме=МЕ/AM=1,73/(корень из 19)=0,3967. Отсюда угол =66гр. 24 мин. Синус этого угла равен =0,92. Отсюда АЕ=АМ*sinАМЕ=4,36*0,92=4. АС=АЕ+ЕС=4+2=6.(поскольку ДЕ=ЕС=АЕ-АД=4-2=2). Отсюда площадь треугольника S=1/2*АС*ВД=1/2*6*3,46=10,38.
См. решение
Объяснение:
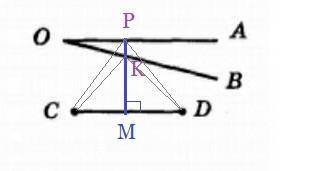
1) Находим середину отрезка CD и отмечаем ее точкой M
2) Через точку M строим перпендикуляр к отрезку CD. Отмечаем точки пересечения перпендикуляра со сторонами <AOB: P и K
3) Докажем что точки P и K равноудалены от C и D.
Рассмотрим ΔCMK и ΔDMK: <CMK = 90° = <DMK, CM = MD по условию, MK - общая сторона для ΔCMK и ΔDMK, => ΔCMK = ΔDMK по двум катетам, => CK = KD, т.е точка K - равноудалена от C и D и точка K лежит на стороне OB <AOB
Аналогично рассмотрим ΔCMP и ΔDMP: <CMP = 90° = <DMP, CM = MD по условию, MP - общая сторона для ΔCMP и ΔDMP, => ΔCMP = ΔDMP по двум катетам, => CP = PD, т.е точка P - равноудалена от C и D и точка P лежит на стороне OA <AOB
как понять? я не понела !