
Sпол=552см²
V=1264√3/3 см³
Объяснение:
Sбок=1/2*(Росн1+Росн2)*ап.
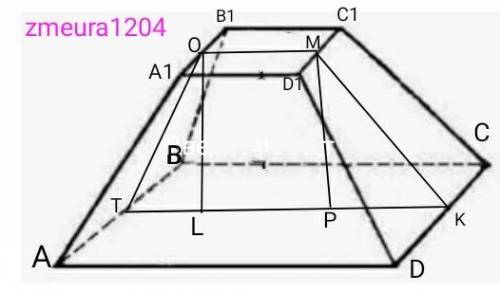
Росн1=А1В1*4=6*4=24см
Росн2=АВ*4=14*4=56см
Sбок=1/2*(24+56)*8=1/2*80*8=320см²
Sосн1=А1В1²=6²=36см²
Sосн2=АВ²=14²=196см²
Sпол=Sбок+Sосн1+Sосн2=320+36+196=
=552см².
МК=8см апофема.
ОМ=В1С1=6см
ТК=ВС=14см.
Трапеция равнобокая.
ТL=PK
PK=(TK-OM)/2=(14-6)/2=4см проекция апофемы на плоскость
∆МРК- прямоугольный треугольник.
По теореме Пифагора
МР=√(МК²-РК²)=√(8²-4²)=√(64-16)=√48=
=4√3 см высота пирамиды.
h=4√3см
V=1/3h(Sосн1+√(Sосн1*Sосн2)+Sосн2)=
=1/3*4√3(36+√(36*196)+196)=
=1/3*4√3*(36+84+196)=4√3/3*316=
=1264√3/3см³
Объяснение:
Сумма углов равна 180°.
Сумма смежных углов равна 180°.
1.
Угол КNM=180°-(35°+25°)=120°
2.
Угол РЕК=180°-(40°+60°)=80°
3.
Угол ТSM=180°-(90°+30°)=60°
4.
Треугольник АВС-равнобдренный, отсюда следует, что углы при основании равны:
Угол АВС=углу ВАС=70°
Угол ВСА=180°-(70°+70°)=40°
5.
В данном рисунке нам дан равносторонний треугольник, так как все стороны равны, а значит что углы тоже равны. Найдём три угла, которые равны:
180°:3=60°
9.
Угол ОМN и угол NMK-смежные.
Угол NMK=180°-130°=50°
Нам дан равнобедренный треугольник, а значит угол NMK=углу NKM=50°
Угол MNK=180°-(50°+50°)=80°
<MNR=<MNO+<ONR=60°+90°=150°
MO=NO=KO=LO=r, KL=MN => ∆MON=∆KOL => <NKL=<MNO=60°
Рассмотрим ∆MON:
ON=MO=r => ∆MON-равнобедренный
Проведём высоту ОН в ∆MON.(она также будет и медианой, т.е. MH=HN=4.7/2=2.35)
Рассмотрим ∆NOH:
∆NOH-прямоугольный, т.к. <NHO=90°, т.к. ОН-высота => <NOH=30° (180-90-60=30, если нужен расчёт) => HN=½ON=½r => r=2HN=2x2.35=4.7 => d=2r=2x4.7=9.4(см)