Question

Скласти рівняння сторін трикутника заданого своїми вершинами А(2;6) В(4;7)
С

Answer 1

Составим уравнения прямых, проходящих через точки А и В, В и С, А и С - это и будут искомые уравнения.

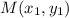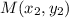Уравнение прямой на плоскости, проходящей через две заданные точки $M(x_1,y_1)$ и $M(x_2, y_2)$, имеет вид $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$.

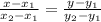Для вершин А и В: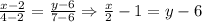 $\frac{x-2}{4-2}=\frac{y-6}{7-6}\Rightarrow \frac{x}{2}-1= y - 6$. Прямая 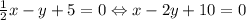$\frac{1}{2} x-y+5=0\Leftrightarrow x-2y+10=0$ - уравнение стороны АВ.

Для вершин В и С: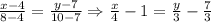 $\frac{x-4}{8-4}=\frac{y-7}{10-7}\Rightarrow \frac{x}{4}-1=\frac{y}{3}-\frac{7}{3}$. Прямая $\frac{1}{4}x-\frac{1}{3}y+\frac{4}{3}=0\Leftrightarrow 3x-4y+16=0$ - уравнение стороны ВС.

Для вершин А и С: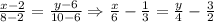 $\frac{x-2}{8-2}=\frac{y-6}{10-6}\Rightarrow \frac{x}{6}-\frac{1}{3}=\frac{y}{4}-\frac{3}{2}$. Прямая 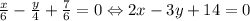$\frac{x}{6}-\frac{y}{4}+\frac{7}{6}=0\Leftrightarrow 2x-3y+14=0$ - уравнение стороны AC.

ОТВЕТ: AB: x - 2y + 10 = 0; BC: 3x - 4y + 16 = 0; AC: 2x - 3y + 14 = 0.