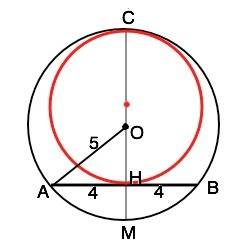
Пусть центр данной окружности О, хорда АВ, диаметр СМ перпендикулярен АВ и пересекает её в середине хорды точке Н. АН=ВН. СО=ОМ - радиусы.
Для второй окружности, хорда АВ - касательная. Следовательно, диаметр СН перпендикулярен АВ и, чтобы быть наибольшим из возможных, должен лежать на диаметре СМ данной окружности.
Соединив О и А, получим прямоугольный ∆ АОН. Этот треугольник -"египетский", катет ОН=3 ( можно проверить по т.Пифагора).
Тогда СН=СО+ОН=5+3=8. Диаметр внутренней окружности СН=8, ее радиус 8:2=4, и S=πr=16π
В равнобедренном треугольнике углы при основании равны, в треугольнике не может быть двух тупых углов, следовательно только угол против основания может равен 120.
Серединный перпендикуляр к основанию равнобедренного треугольника является также биссектрисой - делит угол против основания на два угла по 60, и медианой - делит основание на два отрезка по 3.
Точка пересечения серединных перпендикуляров является вершиной равнобедренного треугольника с основанием на боковой стороне (любая точка серединного перпендикуляра равноудалена от концов отрезка). Равнобедренный треугольник с углом 60 - равносторонний. В равностороннем треугольнике высоты равны.
Расстояние от точки пересечения серединных перпендикуляров до боковой стороны равно 3.