Найдите высоту трапеции, если ее боковые стороны равны корень из 5 и корень из 7, а
основания равны 3 и 6.

👇

Увидеть ответ

Ответ:

degorov152

21.03.2023

≈1.9

Объяснение:

AD=6, BC=3.В трапеции:

AD=AH+ND+BC

Проведем высоты BH и CN:

AH=корень из(5-BH²)

ND=корень из (7-CN²)

CN=BH=x

Тогда:

$6 = \sqrt{5 - {x}^{2} } + \sqrt{7 - {x}^{2} } + 3 \\ x = \frac{ \sqrt{131} }{6}$

Отсюда x≈1.9

4,5(95 оценок)

Ответ:

bitievru2014

21.03.2023

(√131)/6 ед. изм.

Объяснение:

Дано: КМРТ - трапеция, КМ=√5, РТ=√7, МР=3, КТ=6. МН - высота.

Найти МН.

Проведем вторую высоту РВ=МН.

ВН=МР=3, тогда КН+ВТ=6-3=3.

Пусть КН=х, тогда ВТ=3-х.

По теореме Пифагора МН²=МК²-КН² и РВ²=РТ²-ВТ²

МК²-КН²=РТ²-ВТ²

(√5)²-х²=(√7)²-(3-х)²

5-х²=7-(9-6х+х²)

5-х²=7-9+6х-х²

6х=7; х=7/6

КН=7/6

По теореме Пифагора

МН²=МК²-КН²=5 - (49/36) = 180/36 - 49/36 = 131/36

МН=(√131)/6 ед. изм.

4,5(80 оценок)

Открыть все ответы

Ответ:

Ksenya356

21.03.2023

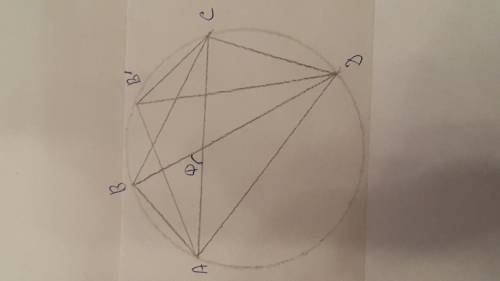
Треугольник АВС, АВ=ВС=10, АС = 16, точка М - точка пересечения биссектрис треугольника - центр вписанной окружности, точка К - цент пересечения серединных перпендикуляров - центр описанной окружности, ВН - высота треугольника на АС, МН - радиус вписанной окружности, ВК - радиус описанной окружности и лежит за пределами треугольника, угол В - тупой,

АН=НС=16/2=8, ВН = корень (АВ в квадрате - АН в квадрате) = корень(100-64)=6

Полупериметр = (10+10+16)/2=18

Площадь треугольника = 1/2АС х ВН = 8 х 6=48

радиус вписанной = площадь/полупериметр = 48/18=2,67 = МН

радиус описанной = произведение сторон / 4 х площадь = 10 х 10 х 16 / 4 х 48= 8,33=ВК

расстояние между центрами = ВК - ВН+МН=8,33-6+2,67=5

4,7(27 оценок)

Ответ:

sasavotchel

21.03.2023

Строго говоря, теорема Птолемея дает необходимое и достаточное условие того, что около четырехугольника можно описать окружность. Но если честно, я ни разу не встречал задачу, в которой пришлось бы использовать достаточность. То есть всегда бывает дано, что четырехугольник вписан в окружность, и отсюда делается соответствующий вывод. Предлагаю в таком виде теорему и формулировать.

Теорема Птолемея.  Если четырехугольник ABCD вписан в окружность, то произведение диагоналей равно сумме произведений противоположных сторон

AC·BD=AB·CD+AD·BC.

Меня всегда удивлял тот факт, что в этой теореме приходится перемножать противоположные стороны. Как-то далеко друг от друга они расположены. Вот если бы соседние перемножались, то никакого предубеждения у меня не возникало бы. Это и дало толчок к моему доказательству.

Найдем площадь ABCD двумя

Во-первых, эта площадь равна половине произведения диагоналей на синус угла между ними - эта формула, как мне кажется, школьникам должна быть известна.

Доказывается она либо разбиением четырехугольника диагоналями на 4 треугольника, либо более красиво - рассматривая его как половину (по площади) параллелограмма, чьи стороны параллельны диагоналям четырехугольника и проходят через его вершины,

Если обозначить угол между диагоналями буквой Ф, то

  S=(1/2)AC·BD·sin Ф

Угол Ф - это угол между хордами AC и BD, а он, как известно из школьной программы, равен полусумме дуг AB и CD, высекаемых этими хордами. Через вписанные углы он выражается в виде суммы углов BCA и CBD. Запомним это.

Во-вторых, более или менее естественно попробовать сосчитать площадь ABCD как сумму площадей двух треугольников, скажем ABC и ADC, но в этом случае мы будем получать произведения соседних сторон, а не противоположных. Выйдем из положения не совсем обычным Отрежем от четырехугольника треугольник ABC (останется нетронутым треугольник ADC) , перевернем ABC другой стороной и "приклеим" на старое место. Если Вы не любите "играть в бирюльки" и хотите "математическое рассуждение", то вот оно. Рассмотрите диаметр окружности, перпендикулярный AC, и рассмотрите точку B', симметричную точке B относительно этого диаметра. Конечно, она снова лежит на окружности, при этом AB=CB'; BC=B'A. Иными словами, мы получили четырехугольник AB'CD, площадь которого равна площади старого, с теми же сторонами, но теперь те стороны, которые были противоположными, стали соседними. Разобьем четырехугольник AB'CD на два треугольника так, чтобы их сторонами были бывшие противоположные. Тогда

S_(ABCD)=S_(AB'CD)=S_(AB'D)+S_(B'CD)=
(1/2)AB'·ADsin DAB'+(1/2)B'C·CDsin B'CD

Во вписанном четырехугольнике, как известно, сумма противоположных углов равна 180°, значит синусы этих углов равны, поэтому

S_(ABCD)=(1/2)(AB'·AD+B'C·CD)sin DAB'=
(1/2)(BC·AD+AB·CD)sin (DAC+CAB')=
(1/2)(BC·AD+AB·CD)sin (DBC+BCA)=
(1/2)(BC·AD+AB·CD)sin Ф

(углы DAC и DBC опираются на одну дугу и поэтому равны,
углы CAB' и BCA опираются на равные хорды B'C и AB и поэтому равны).

Сравнив две полученные формулы для площади ABCD, получаем искомую формулу.

Пример на использование  теоремы Птолемея.

Четырехугольник ABCD вписан в окружность, AB=1, AC=2, AD=6/5, ∠ADC=90°. Найти BD.

Решение. ∠ADC=90°⇒∠ABC=90°, то есть ABCD разбит диагональю AC на два прямоугольных треугольника. С теоремы Пифагора находим неизвестные катеты этих треугольников: BC=√3; CD=8/5.
По теореме Птолемея BD·AC=AB·CD+BC·AD;
2BD=8/5+6√3/5; BD=(4+3√3)/5

Заканчивая сей опус, хочу извиниться за то, что не сейчас сделать чертеж - очень много дел запланировано на этот вечер. Если кто-нибудь сделает мне его - отдам все заработанные на этой задаче .)))
Теорема птолемея с доказательством. альтернативные (нестандартные) доказательства. четкие и разборчи