20/25.
Объяснение:
1) sin²α+ cos²α= 1
sin²α = 1 - cos²α = 1 - (15/25)² = 625/625 - 225/625 = 400/625;
Так как α - угол I четверти, то sinα > 0, тогда
sinα = +√(400/625) = 20/25.
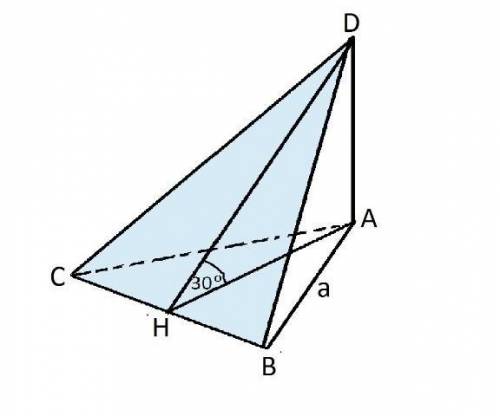
Для решения задачи нужно знать
длину АD, DН и стороны основания,
синус и косинус 30°
АН- высота, медиана и биссектриса треугольника САВ
Треугольник в основании правильный, угол НАВ=60:2=30°
DН=АН:соs 30°
AH=AB*cos 30°=(а√3):2
DН=(а√3):2]:√3):2=а
DА=DН*sin 30°=а/2
Площадь боковой поверхности пирамиды состоит из суммы площадей
треугольника АDВ и 2-х равных треугольников САD и ВАD ( у них равны стороны).
S BDC=DH*CB:2= а*а:2=а²/2
SDAC+S DAB=2*AD*AB:2=2*а²:4=а²/2
Площадь боковой поверхности пирамиды:
S бок =а²/2+а²/2=а²
Не хотела возвращаться в СССР
Марина Цветаева уехала из Советской России в мае 1922 года. Следующие 17 лет она провела в эмиграции вместе с мужем и двумя детьми. Они жили очень бедно, порой на грани голода. Стихи Цветаевой не пользовались успехом среди русских эмигрантов. Вдобавок ее мужа вскоре заподозрили в сотрудничестве с советскими спецслужбами. При всем этом Марина Ивановна не хотела возвращаться на Родину, говоря, что там не осталось ничего, к чему можно было бы вернуться. Однако муж и дочь Ариадна фактически поставили ее перед фактом, что они возвращаются. И уехали. Оставшись одна с сыном-подростком, Марина Цветаева вынуждена была последовать за ними.
cos²x+sin²x=1
(15/25)²+sin²=1
sin²=1-225/625
sin²=400/625
sin= 20/25