
Формула длины высоты через составные отрезки гипотенузы: h = √AO*OC, где АО иОС отрезки,равные 25см и 9см. Тогда высота,проведённая к гипотенузе AС прямоугольного треугольника ABC равна √25*9 = √225 = 15. В прямоугольном треугольнике АВО АВ является гипотенузой, а катеты это отрезок АО = 25 и высота ВО = 15.
Значит гипотенуза АВ треугольника АВО АВ=√25²+15² = √850 = 5√34
Но АВ это как раз больший катет треугольника АВС он равен 5√34
А есть еще теорема о высоте прямоугольного треугольника. Из которой вытекает, что катет
АВ² = АС*АО (квадрат катета равен произведению гипотенузы на прилежащий к этому катету отрезок гипотенузы, на которые высота делит гипотенузу)
Тогда АВ = √34*25 = √850 = 5√34
Прямые ОА и АС - являются секущими по отношению к данной окружности.
Объяснение:
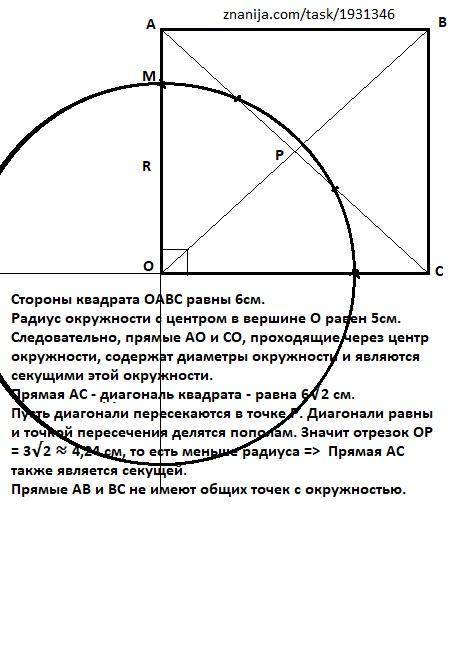
Стороны квадрата ОАВС равны 6см.
Радиус окружности с центром в вершине О равен 5см.
Следовательно, прямые АО и СО, проходящие через центр окружности, содержат диаметры окружности и являются секущими этой окружности.
Прямая АС - диагональ квадрата - равна 6√2 см.
Пусть диагонали пересекаются в точке Р. Диагонали равны и точкой пересечения делятся пополам. Значит отрезок ОР = 3√2 ≈ 4,24 см, то есть меньше радиуса => Прямая АС также является секущей.
Прямые АВ и ВС не имеют общих точек с окружностью.
Да, это параллелограмм
Объяснение:
Потаму что
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Теоремы (свойства параллелограмма):
В параллелограмме противоположные стороны равны и противоположные углы равны
Диагонали параллелограмма точкой пересечения делятся пополам
Углы, прилежащие к любой стороне, в сумме равны
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника являются вершинами параллелограмма Вариньона.
Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника . Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.