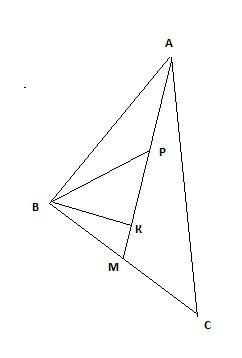
Построим треугольник АВС, площадь которого равна 40 кв. см, Проведем медиану АМ. и обозначим точу Р такую, что АР:РМ=2:3.
Так как медиана треугольника делит его на две равновеликие части, то Sавм=40/2=20 кв. см.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Для наглядности построим высоту ВК – она будет являться высотой как для треугольника ВАМ так и для треугольника ВРМ
Основания Данных треугольников будут соотноситься как 3:5, значит
Sврм : Sвам=3 : 5
Sврм= Sвам*3 / 5=20*3/5=12 кв.см.
Пусть расстояние равно d
Из ∆ADM MD^2 = 10^2-(2x)^2=100-4x^2
Из ∆MDB MD^2 = 17^2-(5x)^2=289-25x^2
100-4x^2=289-25x^2
21x^2=189
x^2=9
x=3