Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 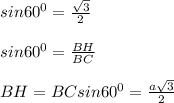
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
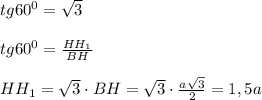
в) Найти площадь боковой поверхности - самая простая часть этого задания:
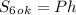 , где
, где 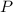 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
Объяснение:
given, cosA + cosB + cosC = 3/2
=> 2(2cos(A + B)/2 . cos(A - B)/2) + 2cosC = 3
=> 2(2cos(pi/2 -c/2) .cos(A - B)/2 + 2(1 - 2sin^2(A/2)) = 3
=> 4sin(c/2) .cos(A - B)/2 + 2 - 4sin^2(A/2)) = 3
=> 4sin^2(A/2) - 4sin(c/2) .cos(A - B)/2 + 1 = 0
This is a quadratic equation in sinc/2, and it has real roots
Therefore , Descriminant >= 0
=> (-4cos(A - B)/2)^2 - 4*4*1 >= 0
=> (cos(A - B))^2 >= 1
=> cos(A - B) = 1, since cosine of any angle can't be > 1
=> A - B = 0
=> A = B
Similarily we can prove that B = C
Thus A = B = C, triangle is equilateral
треугольники, образованные при пересечении диагноалей с вершиной в точке их пересечения и основаниями - основаниями трапеции - подобны. ВС:АД=4:12=1:3. Площади относятся как 1:9. Площадь треугольника ВОС=45:9=5см2.