A B <ADC=60
- - - - <BCD=30
- - - - AB=4√3
- - - - DC=20√3
- - - -
D C
M N
Нехай DM=x см, тоді NC=(20√3-4√3-x)=(16√3-х) см
AM=BN як висота трапеції.
З трикутника BNC-прямокутний BN/CN=tg<BCN, BN=CN·tg30=(16√3-x)·1/√3=
=(16·√3-x)/√3
З трикутника AMD-прямокутний AM/DM=tg<ADM, AM=DM·tg60=x√3
Прирівнюємо
х√3=(16√3-x)·1/√3
3х=16√3-х
4х=16√3
х=16√3/4=4√3
DM=4√3 (см)
З трикутника AMD-прямокутний AM/DM=tg60 AM=4√3·√3=12 (см)
Відповідь: 12 см.
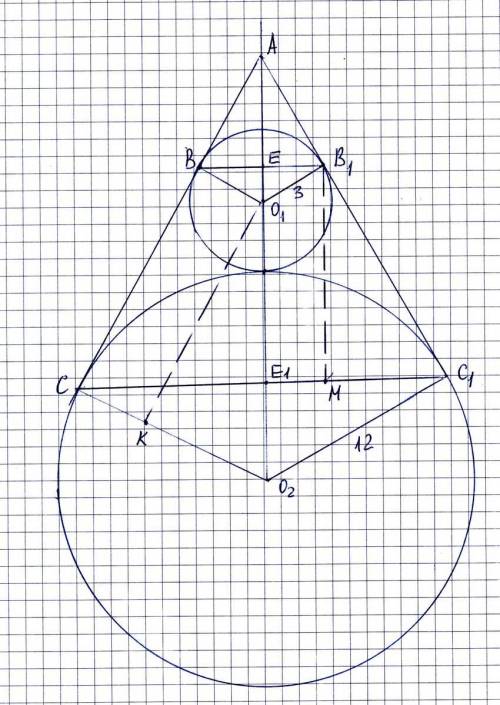
Легко видеть что О1К = 12 = ВС = В1С1, из подобия АВО1 и АСО2 получаем АВ = 4, АС = 16. Из того, что АСЕ1 (и ВЕА!) ТОЖЕ египетский треугольник, подобный (3,4,5), следует, что СЕ1 = АС*3/5 = 48/5, а ВЕ, само собой, в 4 раза меньше, ВЕ = 12/5;
В1М = В1С1*4/5 (все по той же причине!) = 12*4/5 = 48*5.
Осталось все сложить и перемножить
Scbb1c1 = (СЕ1 + ВЕ)*B1M = (48/5 + 12/5)*48/5 = 12*12*4/5 = 115,2
Ну, ответ как ответ, вроде все числа правильные... проверьте.
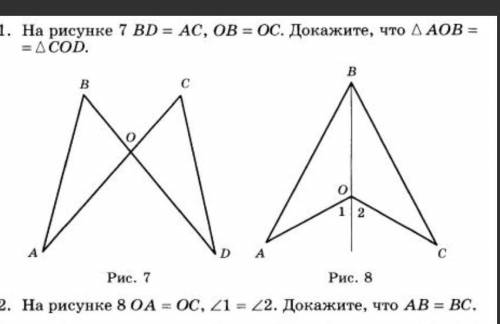
решение на фото
..............