a) (x-2)²+(y-1)²=25
b) (x+4)²+(y-9)²=4
c) x²+(y+2)²=4
Объяснение:
a) Общая формула окружности
(x-a)² + (y-b)² =R² (1), где a и b соответственно абсцисса и ордината центра окружности, а R - радиус окружности.
Очевидно, что центр окружности О находится точно в середине отрезка АВ. Найдем координаты О.
=((Ха+Xb)/2 ; (Ya+Yb)/2) = ( (-1+5)/2; ((-3)+5)/2)= (2;1)
Очевидно , что радиус окружности равен половине длины отрезка АВ, так как АВ в данном случае является диаметром окружности.
Найдем АВ = sqrt ( (Xb-Xa)² + (Yb-Ya)²) = sqrt ((5-(-1))²+ (-3-5)²)=
sqrt(36+64)=10
=> R=AB/2=10/2=5
Подставляем найденные координаты точки О и значение радиуса R=5
в уравнение (1) . Получим:
(x-2)²+(y-1)²=25
b) Здесь координаты центра описанной окружности уже известны, так как центром описанной окружности в равностороннем треугольнике будет являться точка пересечения его медиан О (-4;9)
Длина радиуса же равна 2/3 длины медианы.
Найдем медиану:
Длина стороны : Р:3= 6√3/3=2√3
Тогда длина медианы = 2√3*cos 60° = 2√3*√3/2=3
Тогда 2/3 медианы или радиус описанной окружности равен :
R=2/3*3=2
Подставляем найденные координаты точки О и значение радиуса R=2
в уравнение (1) . Получим:
(x+4)²+(y-9)²=4
c) Центр вписанной в квадрат окружности находится на пересечения диагоналей квадрата, которые точкой пересечения делятся пополам.
Значит нужно найти координаты точки, являющейся серединой диагонали квадрата. Мы используем диагональ АС.
Тогда координаты точки О находим по формуле:
=((Ха+Xс)/2 ; (Ya+Yс)/2) = ( (-1+1)/2; ((-3)+(-1)))/2)= (0;-2)
Радиус вписанной в квадрат окружности будет равен половине его стороны ( возьмем сторону АВ)
АВ= sqrt ( (Xb-Xa)² + (Yb-Ya)²) = sqrt ((-1-(-1))²+ (-1-(-3)²)=
=sqrt(0+16)=4
=>R=AB/2= 4/2=2
Подставляем найденные координаты точки О и значение радиуса R=2 в уравнение (1) . Получим:
x²+(y+2)²=4
Внизу
Объяснение:
Подобны, Если пирамида пересечена плоскостью, параллельной основанию, то:
1) боковые ребра и высота разделены на пропорциональные части;
2) многоугольник сечения подобен основанию;
3) площади основания и сечения относятся, как квадраты их расстояний от вершины.
Доказательство:
1) Так как \beta\||\alpha и они пересечены плоскостью грани ASB по прямым A_{1}B_{1} и AB , то A_{1}B_{1}||AB. Аналогично получим, что B_{1}C_{1}||BC, C_{1}D_{1}||CD и т. д. и B_{1}H_{1}||BH. На сторонах углов ASB, BSC, CSD, ... , BSH получим пропорциональные отрезки:
\frac{SA_{1}}{A_{1}A} = \frac{SB_{1}}{B_{1}B}; \frac{SB_{1}}{B_{1}B} = \frac{SC_{1}}{C_{1}C}; \frac{SC_{1}}{C_{1}C} = \frac{SD_{1}}{D_{1}D}; \ldots ; \frac{SB_{1}}{B_{1}B} = \frac{SH_{1}}{H_{1}H}.
Отсюда:
\frac{SA_{1}}{A_{1}A} = \frac{SB_{1}}{B_{1}B} = \frac{SC_{1}}{C_{1}C} = \frac{SD_{1}}{D_{1}D} =\ldots= \frac{SH_{1}}{H_{1}H}.
2) \triangle{A_{1}SB_{1}}\sim\triangle{ASB}; \triangle{B_{1}SC_{1}}\sim\triangle{BSC}; \triangle{C_{1}SD_{1}}\sim\triangle{CSD}
и т.д. Значит
\frac{A_{1}B_{1}}{AB} = \frac{SA_{1}}{SA}; \frac{B_{1}C_{1}}{BC} = \frac{SB_{1}}{SB}; \frac{C_{1}D_{1}}{CD} = \frac{SC_{1}}{SC} и т.д.
Но правые отношения в этих пропорциях равны между собой на основании только что доказанной первой теоремы, поэтому равны между собой и левые отношения:
\frac{A_{1}B_{1}}{AB} = \frac{B_{1}C_{1}}{BC} = \frac{C_{1}D_{1}}{CD} и т.д.
Т. е. стороны многоугольников A_{1}B_{1}C_{1}D_{1}E_{1} и ABCDE пропорциональны. Соответствующие углы этих многоугольников равны. Следовательно, A_{1}B_{1}C_{1}D_{1}E_{1} \sim ABCDE.
3) Пусть Q и Q' — площади основания и сечения. Имеем:
\frac{Q}{Q'} = \frac{A_{1}B_{1}^2}{AB^2};
Но \frac{A_{1}B_{1}}{AB} = \frac{SA_{1}}{SA} = \frac{SH_{1}}{SH} (по теореме 1), поэтому
\frac{Q}{Q'} = \frac{SH_{1}^2}{SH^2}.
1.Тень от фонарного столба будет 4+8=12м, то есть в 12/4=3 раза больше, чем тень от дерева. Значит и высота столба будет в 3 раза больше дерева, то есть 3*3=9м.
2.Треугольник АВС - прямоугольный.
Докажем это с применением теоремы Пифагора:
41²=40²+9²
1681=1600+81
Значит, АС - гипотенуза.
В прямоугольном треугольнике центр окружности находится посередине гипотенузы, следовательно, радиус окружности равен 41:2=20,5 см.
ответ: 20,5 см
3.(картинка)
4.Опустим из вершины равнобедренного треугольника высоту, которая по известной теореме является медианой и биссектрисой. Тогда из получившихся прямоугольных треугольников найдем, что
sin(α/2) = (x/2)/b = x/(2b), где x - это длина искомого основания. Теперь выразим икс.
x = 2b*sin(α/2).
5.Опускаем перпендикуляр BD на сторону AC.
Проекция AB на AC - это AD= AB cos A; проекция BC на AC - это CD= BC cos C.(Картинка 2)Из теоремы синусов
Объяснение:
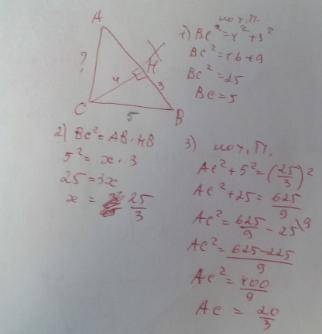
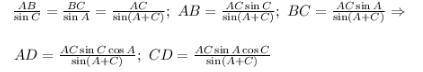
Ол қандай тапсырма екен