См. рисунок в приложении Пусть ребро АА₁ образует со сторонами основания АВ и AD угол в 60°. Соединяем точку А₁ с точкой D. В треугольнике АА₁D AA₁=2 м AD=1 м ∠A₁AD=60° По теореме косинусов A₁D²=AA₁²+AD²-2·AA·₁AD·cos60°=4+1-2·2·1(1/2)=3 A₁D=√3 м Треугольник A₁AD- прямоугольный по теореме обратной теореме Пифагора: АА₁²=AD²+A₁D² 2²=1+( √3 )² A₁D⊥AD В основании квадрат, стороны квадрата взаимно перпендикулярны АС⊥AD Отсюда AD⊥ плоскости A₁CD ВС || AD BC ⊥ плоскости A₁CD
ВС⊥A₁C
A₁C перпендикулярна двум пересекающимся прямым ВС и СD плоскости АВСD По признаку перпендикулярности прямой и плоскости А₁С перпендикуляр к плоскости АВСD A₁C - высота призмы A₁C=Н Из прямоугольного треугольника A₁DC: А₁С²=А₁D²-DC²=(√3)²-1=3-1=2 A₁C=Н=√2 м
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=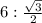 =4√3 см.
=4√3 см.
* * *
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²