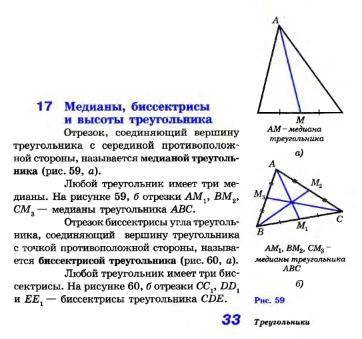
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)
Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)
Любой треугольник имеет:
· три медианы (рис. 59 б)
· три биссектрисы (рис. 60 б)
· три высоты (рис. 62 а, б, в)
Свойства:
- в любом треугольнике медианы пересекаются в одной точке.
- в любом треугольнике биссектрисы пересекаются в одной точке.
- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

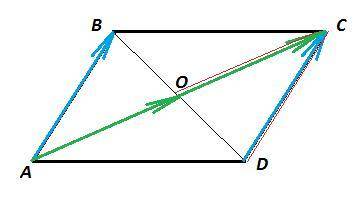
В параллелограмме противоположные стороны попарно параллельны и равны. Диагонали параллелограмма точкой пересечения делятся пополам.
=======================================
1. AB = x*СD; x = 1 - если вопрос касается длин отрезков
x = -1 - если вопрос касается векторов
2. AC = x*AO; x = 2
3. OB = x*BD; x = 0,5 - если вопрос касается длин отрезков
x = -0,5 - если вопрос касается векторов
4. OC = x*CD; определить значение х невозможно, так как длина одной диагонали и длина одной стороны параллелограмма в общем случае никак не связаны.
Частей окружности = 1+3+5 =9
360 : 9 =40
Одна дуга 1 х 40 =40
Вторая - 3 х 40 = 120
Третья - 5 х 40 = 200
Треугольник вписаный , углы , опирающиеся на дугу равны 1/2 дуге
1 угол 40 :2 = 20
2 угол 120 : 2 = 60
3 угол 200 : 2 =100
Всего 180