y = kx + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4Уравнение функции : у = -4х + 5
y = kx + 5 D (6; - 19) ⇒ x = 6 ; у = - 19Подставим значения х,у в уравнение функции:-19 = k * 6 + 5 -6k = 5 + 19-6k = 24k = 24 : (-6)k = - 4Уравнение функции : у = -4х + 5ответ : при k = -4 график функции проходит через точку D(6; -19) .
DB= 1 ед.
Объяснение:
Рассмотрим рисунок. Треугольник Δ АВС - прямоугольный, так как ∠В=90° и равнобедренный, так как АВ=ВС. По условию АВ=ВС=4 ед.
Найдем гипотенузу АС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
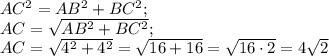
По рисунку понятно, что N- середина АС и тогда отрезок BN - медиана прямоугольного треугольника АВС.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
Значит,
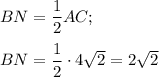
Так как по условию а ⊥ (АВС), то она перпендикулярна любой прямой, лежащей в этой плоскости.
Тогда а⊥ BN и ΔDBN - прямоугольный.
Применим теорему Пифагора и найдем DB.
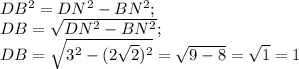
DB= 1 ед.
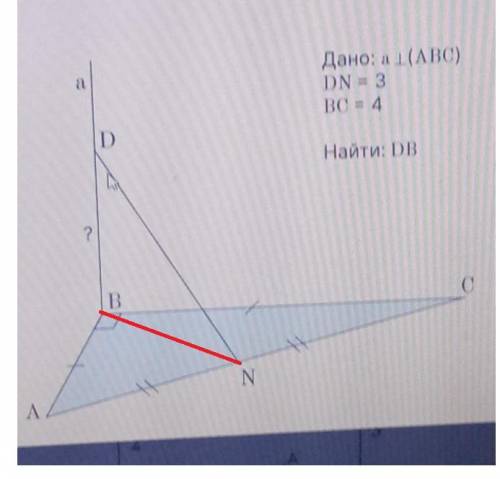
Тут хорошо бы рисунок, но попробую как-то словами.
1. Строится проекция вершины бокового ребра, противолежащего гипотенузе на полоскость основания.
2. Строятся проекции этой вершины НА КАТЕТЫ треугольника в основании (то есть из вершины в плоскости бокового ребра проводится перендикуляр к катету основания).
3. Если внимательно посмотреть на фигуру, вершинами которой являются эти три проекции, а также - вершина прямого угла основания, то это - прямоугольник, в котором проекция бокового ребра на основание - это диагональ.
(Вы должны рассмотреть плоскости, проходящие через перпендикуляр к катету из вершины этого ребра и высоту всей призмы, проведенной из этой же вершины. Поскольку обе прямые перпендикулярны катету в основании, то вся эта плоаскоть перпендикулярна катету, и отрезок, соединяющий проекцию вершины на основание с проекцией этой вершины на катет, тоже перпендекулярен катету - он тоже лежит в этой плоскости. Это справедливо для обеих проекция на катеты. Поэтому там прямоугольник.)
4. Проекции бокового ребра на катеты основания фактически заданы - они равны
p1 = 5*cos(60) [...60 градусов, конечно...] = 5/2;
p2 = 5*cos(45) = 5*√2/2;
5.Это стороны прямоугольника, а диагональ равна
p3 = √(p1^2 + p2^2) = (5/2)*√(2 + 1) = 5*√3/2; (уже видно, что бовокая сторона наклонена к основанию под углом в 30 градусов, но я сейчас получу высоту призмы напрямую)
6. Нам известна длина наклонной 5 и длина её проекции 5*√3/2; поэтому расстояние от вершины бокового ребра до плоскости основания равно 5/2 - по Т.П.
7. Обем призмы равен (8^2/2)*(5/2) = 80