биссектриса делит сторону на пропорциональные отрезки двум другим сторонам
BD=x, DC=10-x
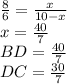
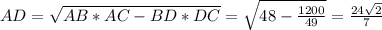
Объяснение:
1)<AOB=<COD как вертикальные, <C =<A(по усл), BO=OD,
тр АОВ=тр ОСД по гипотенузе и острому углу
2)<A=<C, <AOB=<COD(вертикальные), значит и <B=<D,
3) тр. ABD=тр ACD (AD- общая, АВ=CD) по двум катетам,
значит <B=<C
4) тр АВР= тр А1В1Р1 по гипотенузе( АВ=А1В1 ) и острому углу (<1=<2),
тр АВС= тр А1В1С1 по катету(АВ=А1В1) и прилежащему острому углу
(<1=<2) и следовательно тр АРС=тр А1Р1С1 по катету(АР=А1Р1 и гипотенузеАС=А1С1)
5)тр ВРС= тр АКД по двум катетам (ВК=КД, АК=КС)
[ 50 : 10 = 5 ]
В параллелограмме ABCD дано: AD = 2, угол BAD = 60°, ВЕ и AD - перпендикулярны, ВЕ = 2√3. Найдите длину большей диагонали параллелограмма.
Дано: ABCD параллелограмма
AD =2 ; ∠BAD = 60° ;
BE ⊥ AD ; ВЕ = 2√3 . -------
AC - ?
ответ: 2√7
Объяснение: Из ΔABE :
AE =BE*ctg(∠BAD) =2√3*ctg60° =2√3* 1/√3 = 2 = AD
! E совпадает с вершиной D
AB = BD/sin60° = (2√3) / (√3/2) = 4
* * * по другому(чисто геометрическим как катет против угла 30°) AB =2AE и √(AB² - AE²) =BE ⇔ AE√3 =2√3 ⇒ AE =2; AB=4 и E ≡ D * * *
AC² +BD² =2(AB²+AD²) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
AC² =2(4² +2²) - (2√3) ² =40 -12 =28
AC =2√7 .
cм приложение

биссектриса делит угол А пополам, значит угол DAC=45 градусов тогда можем найти катет AC по теореме пифагора AC^2=√BC^2-AB^2=6
тогда треугольник ACD равнобедренный и прямоугольный.
AD/AC=cos45гр
AD=AC*cos45=6*√2/2=3√2