Условие задания: B
П
А
D
Вычисли остальные углы трапеции АО если A 26,
ответ: В .
се срет
ответить!

👇

Увидеть ответ

Открыть все ответы

Ответ:

nalininegi

01.10.2022

$\boxed{CD = 15}$

Объяснение:

Дано: ABCD - трапеция, AB ∩ CD = K, AD = 12, AC = 8,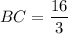 $BC = \dfrac{16}{3}$ , BK = 8

Найти: CD - ?

Решение: Треугольник ΔKBC подобен треугольнику ΔKAD по двум углам, так как угол ∠AKD - общий, а так как по условию ABCD - трапеция, то по определению трапеции её две стороны являются параллельными, так как по условию AB ∩ CD = K, то следовательно BC║AD, тогда угол ∠KBC = ∠KAD как соответственные углы при параллельных прямых и секущей по теореме (BC║AD; AK - секущая). По свойству отрезка AK = AB + BK. Так как треугольник ΔKBC подобен треугольнику ΔKAD по двум углам, то по свойствам подобных треугольников: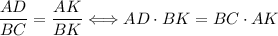 $\dfrac{AD}{BC} = \dfrac{AK}{BK} \Longleftrightarrow AD \cdot BK = BC \cdot AK$ .

$AD \cdot BK = BC \cdot (AB + BK)$

$12 \cdot 8 = \dfrac{16}{3} \cdot (AB + 8 )\bigg | \cdot 3$

288 = 16(AB + 8)|:16

18 = AB + 8

AB = 10

Рассмотрим треугольник ΔABC. ПО теореме косинусов:

$BC^{2} + AC^{2} - 2 \cdot BC \cdot AC \cos \angle ACB = AB^{2}$

$\cos ACB = \dfrac{BC^{2} + AC^{2} - AB^{2}}{2 \cdot BC \cdot AC} = \dfrac{\left (\dfrac{16}{3} \right)^{2} + 8^{2} - 10^{2}}{2 \cdot \dfrac{16}{3} \cdot 8} = \dfrac{\dfrac{256}{9} + 64 - 100 }{\dfrac{256}{3} } =$

$= \dfrac{\dfrac{256}{9} - 36 }{\dfrac{256}{3} } = \dfrac{\dfrac{256}{9} - \dfrac{324}{9} }{\dfrac{256}{3} } = \dfrac{\dfrac{256 - 324}{9} }{\dfrac{256}{3} } = -\dfrac{\dfrac{68}{9} }{ \dfrac{256}{3} } = - \dfrac{68 \cdot 3}{256 \cdot 9} = -\dfrac{68}{768} = -\dfrac{17}{192}$ .

Угол ∠ACB = ∠CAD как внутренние разносторонние углы при при параллельных прямых и секущей по теореме (BC║AD; AK - секущая).

Так как ∠ACB = ∠CAD, то cos ∠ACB = cos ∠CAD.

По теореме косинусов для треугольника ΔCAD:

$CD = \sqrt{AC^{2} + AD^{2} - 2 \cdot AC \cdot AD \cos \angle CAD} = \sqrt{8^{2} + 12^{2} - 2 \cdot 8 \cdot 12\cdot \left (- \dfrac{17}{192} \right)} =$ $= \sqrt{64 + 144 + 17} = \sqrt{225} = 15$ .

4,6(100 оценок)

Ответ:

Сафина3651

01.10.2022

ответ: 3,21см²

Объяснение: известно, что периметр нашего ромба 16см, значит длина одной стороны будет:16/4=4см.

Найдем сторону подобного ромба. Известны его диагонали. Диагонали в точке пересечения делятся пополам и образуют 4 прямоугольных треугольника с катетами 4 и 8 см. Боковая сторона находится по теореме Пифагора: √4²+8²=√16+64=√80=8,9см.

Отношение сторон подобного ромба к нашему равно: 8,9/4=2,23.

Находим диагонали нашего ромба: d1=4/2,23=1,79 см. d2=8/2,23=3,59см.

Находим площадь нашего ромба: S=1/2*d1*d2=0,5*1,79*3,59=3,21см²

4,6(89 оценок)

Это интересно:

13.09.2021

Как всегда выигрывать спор...

Компьютеры-и-электроника

09.07.2020

Как уничтожить жесткий диск: советы и рекомендации...

Компьютеры-и-электроника

20.11.2020