34°
Объяснение:
1) Обозначим один из углов х, тогда второй угол - 3х.
Составим уравнение и найдём углы:
х + 3х = 136°
4х = 136°
х = 136° : 4 = 34° - меньший угол
3х = 34° · 3 = 102° - больший угол.
2) Биссектриса делит угол АОВ на 2 равных угла, каждый из которых равен:
136° : 2 = 68°
3) Больший из двух углов, образованных лучом ОС (угол 3х), образует с биссектрисой угол:
102° - 68° = 34°
4) Меньший из двух углов, образованных лучом ОС (угол х), образует с биссектрисой угол:
68° - 34° = 34°
ответ: угол, образованный лучом OC и биссектрисой угла AOB, равен 34°.
Дан равнобедренный треугольник ABC ( AB = BC ).
Биссектриса AE пересекает высоту BD в точке О, причем OB/OD=3/1 .
Пусть АВ = ВС = х, АD = DC = y.
Используем свойство точки пересечения биссектрис.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
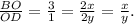
Отсюда следует х = 3у.
По Пифагору х² = у² + (3 + 1)². Зваменим у.
(3у)² = у² + 4²,
8у² = 16,
у = √(16/8) = √2.
Переходим к углам.
Угол OAD = ABD как взаимно перпендикулярный.
tg OAD = tg ABD = √2/4.
Находим ОК = AD*tg OAD = √2*(√2/4) = 2/4 = 0.5.
Отрезок ВК = 4 - 0,5 = 3,5.
ответ: ВК/KD = 3,5/0,5 = 7/1.

24*2=48
62-48=14 это бок.сторона 1
24 +24 +14+14=76 пиреметр прямоугольника