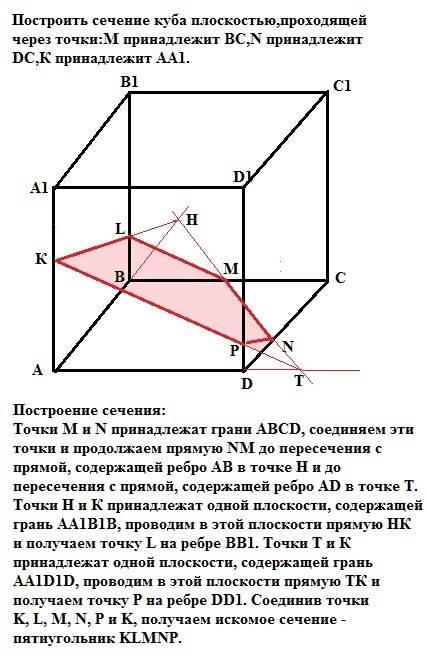
Построение сечения:
Точки M и N принадлежат грани АВСD, соединяем эти точки и продолжаем прямую NM до пересечения с прямой, содержащей ребро АВ в точке Н и до пересечения с прямой, содержащей ребро AD в точке Т. Точки Н и К принадлежат одной плоскости, содержащей грань АА1В1В, проводим в этой плоскости прямую НК и получаем точку L на ребре ВВ1. Точки Т и К принадлежат одной плоскости, содержащей грань АА1D1D, проводим в этой плоскости прямую ТК и получаем точку Р на ребре DD1. Соединив точки K, L, M, N, P и K, получаем искомое сечение - пятиугольник KLMNP.
Компас-это прибор для определения горизонтальных направлений на местности. Применяется для определения направления, в котором движется морское, воздушное судно, наземное транспортное средство; направления, в котором идет пешеход; направления на некоторый объект или ориентир. Компасы подразделяются на два основных класса: магнитные компасы типа стрелочных, которыми пользуются топографы и туристы, и немагнитные, такие, как гирокомпас и радиокомпас.
Также, компас-прибор для определения стран света (с намагниченной стрелкой, всегда указывающей на север).
Существуют несколько различных видов компаса: магнитный компас, гирокомпас, горный компас, астрономический компас, а также компасы, ориентирующиеся на положение искусственных объектов: радиокомпас, спутниковый компас.
Прототип современного компаса был изобретен итальянцем Флавио Джойя в XIV веке (называют даже точный год - 1302). До этого компас служил лишь для определения направления север-юг. А Джойя предложил делить круг компаса на 16 частей (румбов) для определения других сторон света.
/|
/ |
гипотенуза / |катет
/ |
/__|
катет
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует, что:
если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Из второго признака равенства треугольников следует, что:
если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Рассмотрим еще два признака равенства прямоугольных треугольников:
если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство. Из теоремы о сумме углов треугольника следует, что в этих треугольниках два других острых угла также равны, поэтому они равны по второму признаку равенства треугольников, т. е. по стороне (гипотенузе) и двум прилежащим к ней углам.
|