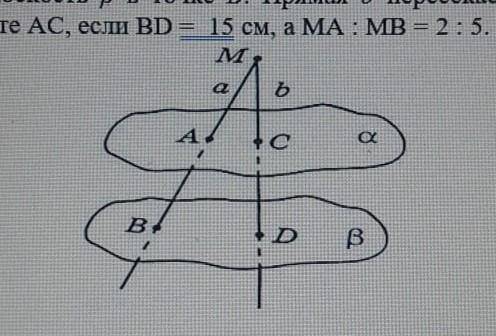
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
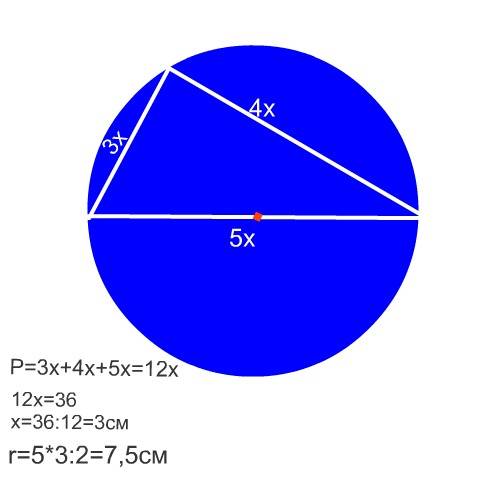
α || β
a ⋂ b = M
a ⋂ α = A
a ⋂ β = B
b ⋂ α = C
b ⋂ β = D
BD = 15
MA : MB = 2 : 5
Найти:
АС - ?
Решение.
Прямые а и b образуют плоскость, которая перескает плоскости α и β. Так как α || β, то АС || BD (по свойству). Рассмотрим ΔMAC и ΔMBD. Они подобны, так как угол М - общий, а угол MAC = углу MBD как соответственные при параллельных прямых. Так как треугольники подобны, из стороны будут пропорциональны. Тогда:
МА : МВ = AC : BD
2 : 5 = AC : 15
AC = 15 * 2 / 5 = 30 / 5 = 6.
ответ: АС = 6 ед.