если разрезать данный треугольник пополам - по высоте, то получатся два прямоугольных треугольника, в которых
a=катет1= высота =6
b=катет2= половина основания =(х+6)/2
c=гипотенуза =боковая сторона = х
по теореме Пифагора
c^2 = a^2 +b^2
x^2 = 6^2 +((х+6)/2)^2
x^2 = 36 +(х+6)^2/4 - домножим обе части на 4
4x^2 = 144 +(х+6)^2
4x^2 = 144 +х^2+24x+36
4x^2 -х^2-24x-180=0
3x^2 -24x-180=0 - делим на 3
x^2 -8x-60=0
квадратное уравнение
D= 304
x1=4-2√19 < 0 - по смыслу не подходит
x2=4+2√19 - боковая сторона
6+x2 =6+4+2√19=10+2√19 или 2(5+√19) - основание
1) 5+10 = 15 см - длина АВ
2) 15²-12²=ВС². (По теореме Пифагора) 225-144=81, ВС =√81=9 см (ВС=9 см)
3) Площ. АВС находим так (АС*ВС)÷2 , т.е. (12*9)÷2=54 см²
Теперь надо найти площ. треугольника МВК и вычесть ее из площ. АВС.
4) Т.к. углы АСВ и МКВ - прямые, а АВ=10 см, что составляет 2/3 от АВ, то ВК равно 2/3 от ВС, т.е. 6 см. ВК=6 см.
5) По теор. Пифагора МВ²-ВК²=МК², т.е 100-36=64, МК-√64=8 см
6) Площ. МВК находим так (МК*ВК)÷2 , т.е. (8*6)÷2= 24 см²
7) Площ. четырехугол. АМКС = 54-24=30 (30 см²)
Формулы:
Обозначим, что X - угол А; Y - угол В (нам уг. С не нужен).
sinX =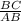
cosX =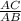
tgX =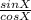
Также и с "Y". Только подставлять другие стороны.
AC = 15, BC = 8, AB - ?
Найдем АВ по т. Пифагора:
AB =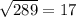
Ищем косинусы,синусы и тангенсы.
sinX = 8 / 17 =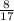
cosX =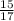
tgX =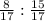 =
= 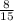
...
sinY =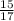
cosY =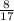
tgY =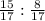 = \
= \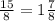
P.S. за 2 месяца я немного забыл, что синусы вроде так ищутся. Я впервые сталкиваюсь, что у меня вот такие дроби получаются. Если будет ошибка - уведомляй. Рисунок я добавил, чтобы не запутаться.