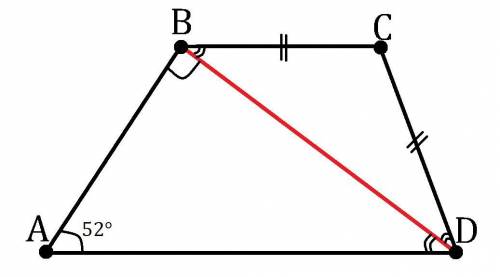
Дано: BC║AD; BD⊥AB; ∠BAD=52°; BC=DC.
Найти: ∠ABC, ∠BCD и ∠CDA.
∠BAD+∠ADB+∠DBA = 180° как сумма углов ΔBAD.
∠ADB = 180°-∠DBA-∠BAD = 180°-90°-52° = 38°
∠ADB = ∠DBC как накрест лежащие углы при параллельных прямых BC, AD и секущей DB.
∠DBC = ∠ADB = 38°.
ΔBCD - равнобедренный (по условию BC=DC), поэтому углы при его основании равны (∠DBC=∠BDC).
∠BDC = ∠DBC = 38°.
∠BCD = 180°-∠BDC-∠DBC = 180°-38°-38° = 104° т.к. сумма углов в треугольнике равна 180°.
∠ABC = ∠DBA+∠DBC = 90°+38° = 128°.
∠CDA = ∠ADB+∠BDC = 38°+38° = 76°.
ответ: 128°, 104° и 76°.
Диаметр окружности, вписанной в ромб, равен его высоте.
а) Высота ромба, проведенная из тупого угла, является катетом прямоугольного треугольника, противолежащим углу 30°, с гипотенузой 10 см и равна её половине.
h=10:2=5 см. d=5 см, r=5:2=2,5 см
или
б) Высоту найдем из площади по одной из формул площади параллелограмма.
S=a•b•sinα, где а и b- стороны, α- угол между ними.
S=10•10•1/2=50 см²
h=S:a=50:10=5см ⇒
r=d:2=2,5 см