
Средняя линия треугольника параллельна стороне треугольника и равна ее половине . В условии не сказано, параллельно какой из сторон проведена средняя линия MN, поэтому может быть два варианта решения.
1 вариант:
MN параллельна основанию RS, RF=SF, RS+2*RF=30 (дано). Тогда
RS=8, а RF=(30-8):2=11.
2 вариант:
MN параллельна боковой стороне RF. Тогда
RF=SF=8, а RS=30-2*8=14.
Оба варианта удовлетворяют условию существования треугольника (теорема о неравенстве), так как большая сторона меньше суммы двух других сторон.
Объяснение:
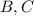 отрезки
отрезки 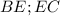 , где точка
, где точка 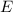 пересечение с окружностью. Обозначим точку перпендикуляра
пересечение с окружностью. Обозначим точку перпендикуляра 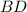 с
с 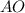
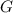 .
. 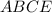 , который вписан в окружность.
, который вписан в окружность. 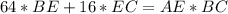 , так как
, так как 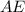 лежит на центре , то треугольники
лежит на центре , то треугольники 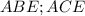 прямоугольные.
прямоугольные.  .
. 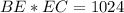 .
. 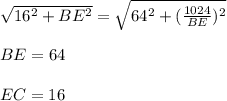
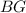 - высота прямоугольного треугольника
- высота прямоугольного треугольника 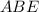 , тогда
, тогда 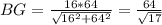 .
.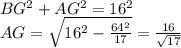 , так как
, так как 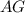 является высотой прямоугольного треугольника
является высотой прямоугольного треугольника 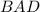 , то
, то 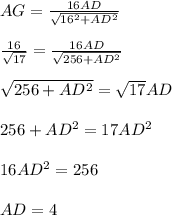
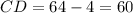
По готовому чертежу нахождение сторон в четырехугольнике.
Объяснение:
1) ΔАВD-прямоугольный ,
tgα= ,
,  .
.
sinα= ,
,  .
.
2) ΔDCB , ∠CDB=180-(β+Y) , sin ∠CDB=sin(180-(β+Y))=sin(β+Y) .
a) по т. синусов , CD=
, CD=  =
= ,
,
CD= .
.
b) по т синусов , BC=
, BC= =
= ,
,
BC=