Дан равнобедренный треугольник ABC ( AB = BC ).
Биссектриса AE пересекает высоту BD в точке О, причем OB/OD=3/1 .
Пусть АВ = ВС = х, АD = DC = y.
Используем свойство точки пересечения биссектрис.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
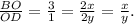
Отсюда следует х = 3у.
По Пифагору х² = у² + (3 + 1)². Зваменим у.
(3у)² = у² + 4²,
8у² = 16,
у = √(16/8) = √2.
Переходим к углам.
Угол OAD = ABD как взаимно перпендикулярный.
tg OAD = tg ABD = √2/4.
Находим ОК = AD*tg OAD = √2*(√2/4) = 2/4 = 0.5.
Отрезок ВК = 4 - 0,5 = 3,5.
ответ: ВК/KD = 3,5/0,5 = 7/1.

Стороны равны: 2 см; 4,5 см; 2 см; 4,5 см;
углы равны: 64°; 116°; 64°; 116°.
Объяснение:
Задание
Диагонали четырехугольника равны 4 см и 9 см, а угол между ними равен 64°. Найдите стороны и углы четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение
Согласно теореме Вариньона, середины сторон произвольного четырёхугольника являются вершинами параллелограмма.
Так как полученный четырёхугольник является параллелограммом Вариньона, то:
1) его противоположные стороны попарно равны и равны 1/2 соответствующей диагонали:
АВ = СD = 4 : 2 = 2 см
ВС = AD = 9 : 2 = 4,5 см;
2) углы между сторонами параллелограмма Вариньона равны углам между диагоналями исходного четырёхугольника:
∠DAB = ∠DCB = 64°
∠ABC = ∠ADC = 180°-64° = 116°
стороны равны: 2 см; 4,5 см; 2 см; 4,5 см;
углы равны: 64°; 116°; 64°; 116°.
Что-то маловато вершин у куба Вашего))
Вероятно, он таков: АВСДА1В1С1Д1. Ага?)
Тогда АВ1 - диагональ грани АВВ1А1.
Расстояние между прямыми должно быть отрезком, перпендикулярным обеим этим прямым.
Очевидно, что он (отрезок этот) лежит в плоскости этой самой грани. Больше того: это высота прямоугольного треугольника АВВ1, в котором АВ1 - гипотенуза.
И еще лучше: пусть точка пересечения этого отрезка с АВ1 будет называться О.
Тогда возникает чудесный равнобедренный прямоугольный треугольник АОВ, где АО и ОВ катеты (притом равные друг другу), а АВ - гипотенуза.
Для него катет посчитать - одно удовольствие:
пусть катеты АО=ОВ=а
тогда
два "а" в квадрате (два квадрата катета) равно квадрату гипотенузы, то есть квадрат "2 КОРНЯ ИЗ 2", что равно восьми
Значит квадрат катета равен половине от восьми, то есть четырем
Значит катет равен корню из четырех, то есть двум!
Это и есть расстояние между прямыми АВ1 и ВС
Ура!))