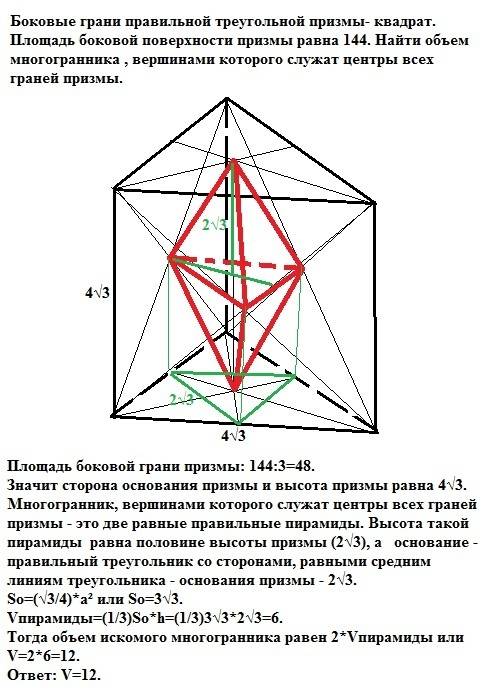
С РИСУНКАМИ В параллелограмме АВСD, AD=6см, угол А=40°. Чему равна сторона ВС и угол С?
2.В прямоугольнике ABCD диагонали пересекаются в точке О. Сторона АС=18см, АВ=17см. Определите периметр треугольника СОD.
3.Диагонали ромба пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNP=80°.
Так как прямые па аралелльны , то четырёхугольники LMXA , MNBZ , MWCY параллелограммы .
Значит AL=XM , MY=WC , MX=BN .
Полученные три треугольника подобны между собой , получаем
(LN/MX)^2 = (27/12)
(ZW/MY)^2 = (3/12)
(MZ/LN)^2 = (3/27)
LN/MX=3/2
ZW/MY=1/2
MZ/LN=1/3
Откуда LN+AL = LN+MX = 5MX/2
Из подобия треугольников NML и ANY получаем
(LN/(LN+AL))^2 = 27/(27+S(ALMX) + 12)
Или 9/25 = 27/(39+S(ALMX))
Откуда S(ALMX) = 36
Аналогично и с двумя другими S(MNBZ)=18 , S(MYCW) = 12
Значит
S(ABC) = 27+12+3+36+18+12 = 108