Объяснение:
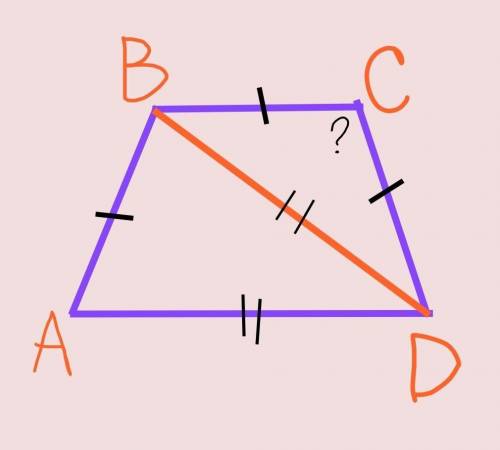
Так как BС=СD по условию, то ∆BCD – равнобедренный с основанием BD. Следовательно угол СВD=угол CDB как углы при основании равнобедренного треугольника.
Сумма углов любого треугольника равна 180°.
Исходя из этого угол ВСD=180°–угол CBD–угол СDB=180°–x–x=180°–2x
Пусть угол СВD=x, тогда угол CDB=х так же.
Основания трапеции параллельны, тоесть ВС//AD.
Тогда угол CBD=угол ADB как накрест лежащие при параллельных прямых ВС и AD и секущей BD.
Так как СВD=x, то угол ADB=x так же.
Так как BD=AD по условию, то ∆АВD – равнобедренный с основанием АВ. А углы при основании равнобедренного треугольника равны. Сумма углов в любом треугольнике равна 180°.
Исходя из этого: угол ABD=(180°–угол ADB)÷2=(180°–x)÷2
Угол АВС=угол ABD+угол CBD=(180°–x)÷2+x
Так как АВ=CD по условию, то трапеция ABCD – равнобедренная.
Углы при основании равнобедренной трапеции равны, тоесть: угол АВС=угол BCD.
Подставим величины этих углов, получим уравнение:
(180–x)÷2+x=180–2x
90–0,5х+х=180–2х
–0,5х+х+2х=180–90
2,5х=90
х=36
Тогда угол ВСD=180°–2*36°=108°
ответ: 108°
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках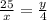
, но х=20-у ⇒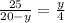 
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.