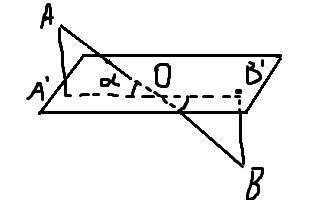
Опустим перпендикуляры из концов отрезка АВ - это и будут искомые расстояния.
Треугольник OAA' - прямоугольный, катет AA' лежит напротив угла α = 30° - значит, он равен половине гипотенузы, т.е. AA' = AO/2.
Прямоугольные треугольник OAA' подобен прямоугольному треугольнику OBB' по острому углу (∠AOA' = ∠BOB' как вертикальные). Поскольку AO : OB = 1 : 2, то AA' : BB' = 1 : 2, т.е. BB' = 2AA' = AO.
Определим длину AO. Пусть AO = x. Тогда OB = 2x.
x + 2x = 45 ⇒ x = 15.
Следовательно, АО = BB' = 15. Тогда AA' = 15 : 2 = 7,5.
ОТВЕТ: 7,5 см; 15 см.
Объяснение: ЗАДАНИЕ 1
Площадь шара вычисляется по формуле:
S=4πR², где R- радиус шара=13+6+8=27
S=4π×27²=4π×729=2916(ед²)
Объем шара вычисляется по формуле:
V=4/3πR³=4/3π×27³=4/3π×19683
=26244π(ед³)
ЗАДАНИЕ 2
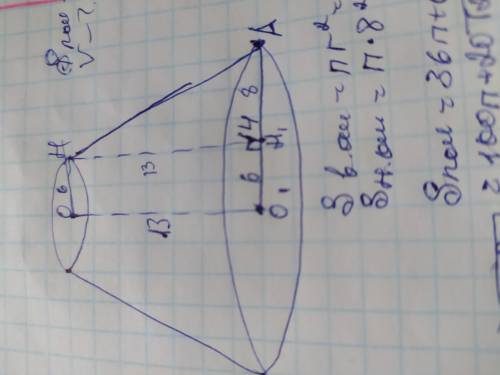
Обозначим радиусы конуса ОН и О1А. Получилась прямоугольная трапеция ОНАО1. Проведём высоту НН1 к радиусу нижнего основания О1А. Она делит О1А так, что О1А=ОН=6, значит Н1А=14-6=8.
Также получился прямоугольный треугольник НАН1, в котором радиусы основания являются катетами а образующая конуса гипотенузой. Найдём НА по теореме Пифагора:
НА²=НН1²+НА²=13²+8²=169+64=233;
НА=√233
Найдём площадь боковой поверхности конуса по формуле:
Sбок=π(R+R1)HA=π(6+14)×√233=20√233π;
√233≈15,3; 20×15,3π=306π
Найдём площадь верхнего и нижнего оснований по формуле: S=πr²
Sверх.осн=π×6²=36π
Sниж.осн=π×14²=196π
Площадь полной поверхности конуса- это сумма всех его площадей основания и боковой поверхности:
Sпол=Sбок.пов+S2хосн=306π+36π+196π==538π
Sпол=538π
Объём усечённого конуса вычисляется по формуле: V=⅓×πH(R1²+R1×R2+R2²)=
=⅓π×13(6²+6×14+14²)=13π/3(36+84+196)=
=13π/3×316=4108π/3(ед³)
или 1369π целых ⅓
ОТВЕТ: Sпол=538π(ед²); V=4108π/3(ед³)
Найдем диагонали квадратовАВСД и А₁В₁С₁Д₁.
АС=6√2, А₁С₁=2√2
Рассмотрим трапециюАА₁С₁С.Опустим высоту из вершин А₁ и С₁ на АС, получим перпендикуляры А₁Н и С₁К .Трапеция равнобокая, поэтому АН=СК=(АС-А₁С₁)/2=(6√2-2√2)/2=2√2.
Рассмотрим ΔАА₁Н. По теореме Пифагора А₁Н²=АА₁²-АН²=26²-4·2=676-8=668,
А₁Н=√668=2√167