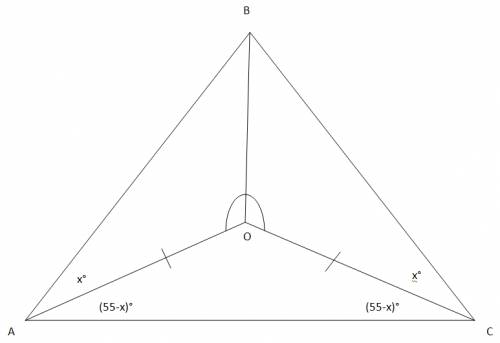
См. рис.
Пусть угол OAB = Х градусов, тогда угол OAC = 55-х градусов
АОС - равнобедренный треугольник, а у равнобедренного треугольника углы при основании равны.
Треугольники AOB и BOC равны по двум сторонам и углу между ними, следовательно соответственные углы равны.
1. ответ: угол ACB = 55 градусов
2. Точки О и В равноудалены от точек А и С (АВ = ВС, так как треугольники AOB и BOC равны), следовательно точки О и В лежат на серединном перпендикуляре к отрезку АС, а прямая ВО - серединный перпендикуляр к стороне АС.
Внешний угол любого внутреннего угла А равен 180 - А, то есть равен сумме двух других углов В + С.
Получаем такие равенства:
{ A + B + C = 180
{ B + C = 2x
{ A + C = 5x
{ A + B = 8x
Если сложить три последних равенства, то получим
2A + 2B + 2C = 2x + 5x + 8x
2(A + B + C) = 15x
2*180 = 15x
x = 24
2x = 48, 5x = 120, 8x = 192
Проверим, углы треугольника
A = 180 - (B + C) = 180 - 48 = 132
B = 180 - (A + C) = 180 - 120 = 60
C = 180 - (A + B) = 180 - 192 = -12
A + B + C = 132+60-12=180