
Объяснение:
Уравнение окружности имеет вид:
(x-x0)²+(y-y0)²=r²
Где (х0;у0) - координаты центра. r- радиус.
Подставив вместо х и у координаты данных точек получаем систему трех уравнений с тремя неизвестными:
для упрощения записи, вместо х0 напишу х, а вместо у0 напишу у:
(-3-x)²+y²=r²
(1-x)²+(3-y)²=r²
(5-x)²+y²=r²
вычтем из первого уравнения третье:
(-3-x)²-(5-x)²=0
9+6x+x²=25-10x+x²
16x=16
x=1
тогда получаем :
16+y²=r²
(3-y)²=r²
16+y²-(3-y)²=0
16+y²=9-6y+y²
6y=-7
y=-7/6
Тогда r²=820/49
Итак уравнение окружности имеет вид:
(x-1)²+(y+7/6)²=820/49
Векторы РК и MN не лежат на одной прямой , причем вектор MN=2РК , |PK|=12 . Найдите |DF| ,если D и F- середины отрезков РМ и NK.
Объяснение:
Т.к. вектор MN=2РК , и они не лежат на одной прямой ⇒ лежат на параллельных прямых .
В 4-х угольнике MNKP две стороны параллельны , две другие нет ⇒ MNKP-трапеция.
Т.к. D-середина РМ , F-середина NK ⇒DF-средняя линия трапеции.
DF=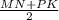 . По условию вектор MN=2РК, значит вектор MN=24.
. По условию вектор MN=2РК, значит вектор MN=24.
DF=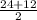 =18 (см).
=18 (см).