32 cм²
Объяснение:
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:
Sбок= 1/2*(Р1+Р2)*L,
где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)
Найдём стороны оснований правильной четырехугольной усеченной пирамиды.
Диагональ квадрата: d = a√2, где а - сторона квадрата.
⇒ а = d/√2
АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.
Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.
Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.
Найдем апофему L
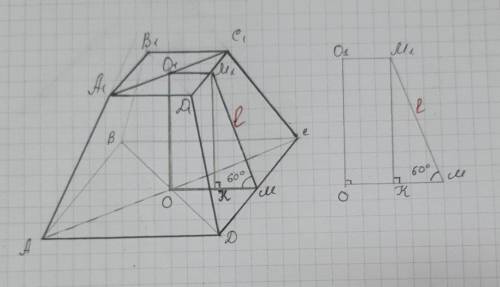
Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.
Т.к. r=a /2 (половина стороны основания), то
О1М1= А1Д1/2 = 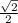
ОМ = АД/2 = 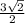
Опустим перпендикуляр М1К из точки М1 верхнего основания на нижнее основание. Получим прямоугольный ΔМ1КМ.
Т.к. М1К⊥КМ, КМ⊥ДС, то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).
КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1= 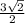 -
- 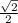 =
=  см.
см.
Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° =  :
: 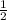 = 2
= 2 cм
cм
Sбок = 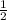 * ( 12
* ( 12 + 4
+ 4 ) * 2
) * 2 =
=  (12+4)
(12+4)  = 2*16=32 cм²
= 2*16=32 cм²
1)Периметр ромба равен 4*сторона
сторона= 52\4=13 см
Площадь ромба равна произведению квадрата стороны на синус угла между сторонами
отсюда синус угла =площадь робма разделить на квадрат стороны
sin A=120\(13^2)=120\169
Так как угол А -острый,то cos A=корень(1-sin^2 A)=корень(1-(120\169)^2)=
=119\169
По одной из основных формул тригонометрии
tg A=sin A\cos A=120\169\(119\169)=120\119
ответ:120\169,119\169,120\119.
2)
Катеты треугольника относятся друг к другу как 9 к 40.
Пусть длина одного катета 9х, тогда второго 40х.
По теореме пифагора квадрат катетов равен квадрату гипотенузы
(9х) в квадрате + (40х) в квадрате = 82 в квадрате
81 х^2 + 1600 х^2 = 6724. Отсюда х^2 = 4.
х=2.
один катет 9х=18 см
второй катет 40х=80 см
3)
Боковые стороны: (36-10)/2=13
Высота h=корень(169-25)=12
tga=5/12 sina=5/13 cosa=12/13.
4) cos - отношение прилежащего( в данном случае неизвестного) катета к гипотенузе, пусть гипотенуза - х, тогда катет 24х / 25. по теореме пифагора квадрат гипотенузы равен сумме квадратов катетов x^2=14^2+(24x / 25)^2, отсюда х=50, а второй катет равен 48