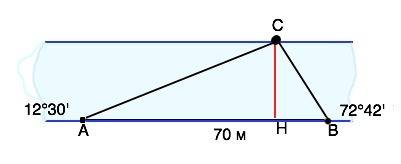
Ширина реки равна длине расстояния СН, измеренного перпендикулярно между ее берегами, иначе - высоте СН треугольника АВС. .
Алгоритм решения:
а) По т.синусов вычислим АС,
б) вычислим площадь ∆ АВС.
в) из площади найдем высоту СН, равную ширине реки.
—————
а ) Угол С=180°- (угол А+угол В)
угол А=12°30’=12,5°
B=72°42’=72,8°
Угол С=180°-(12,5°+72,8°=94,8°
АВ:sin 72,8=AC:sn 94,8°
sin 72,8=0.95476
sin94,8°=0.99649 , откуда АВ=67.0684
б) S (ABC)=AC•AB•sin(CAB):2
S (ABC)=508
CH=2S:AC=1016:70=14,5 м
Треугольник CDE прямоугольный Угол Е = 90-30=60, биссектриса EF делит угол Е на две равные части=30, угол Е=углу FED=30, треугольник DEF - равнобедренный.
Биссектриса делит противоположную сторону на отрезки пропорцианальные двум другим сторонам
СЕ = х и лежит напротив угла 30, значит гипотенуза = 2х =DE.
DE/CE=DF/CF
2x/x =DF/CF
2=DF/CF
2 CF = DF