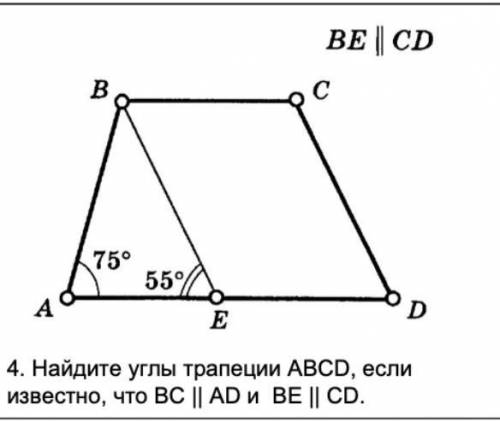
см чертеж. Пардон, я поменял точки В и С местами, уж простите.
У меня обозначено катет АВ = 12, а катет ВС=5. Гипотенуза обозначена АС. Ясно, что она равна 13 (это Пифагорова тройка 5;12;13), и окружность проходит через точки А и С.
Окружность проходит через точки А и С, и к тому же в точке С - касается (не может она в другой точке касаться, а в этой пересекать :))) так не бывает). То есть центр окружности лежит на пересечении перпендикуляра к ВС в точке С и перпендикуляра к АС в точке М - середине АС(то есть такая точка - единственная). Осталось найти на перпендикуляре из точки С к ВС такую точку О, что АО = ОС = R.
На рисунке приведено решение, суть его такова - проводим из О препендикуляр к АВ, получаем прямоугольник со сторонами R и ВС.
(АВ - R)^2 + BC^2 = R^2;
AC^2 = 2*AB*R; R = AC^2/(2*AB).
R = 13^2/24 = 169/24.
FC имеется в виду AC? Если да, то площадь четырёхугольника можно найти как половину произведения его диагоналей на синус угла между ними. Диагонали известны АС=8см, AD=9см, найдём меньший угол между ними. Полный угол (окружность) составляет 360град. на него приходится 2+17+4+13=36 частей, т.е. на 1 часть приходится 360:36=10град. Вписанный угол равен половине величины дуги, на которую он опирается, следовательно./САД=1/2СД, /САД=1/2·4·10=20град, /ВДС=1/2АВ, /ВДС=1/2·2·10=10град. Точка О - точка пересечения диагоналей, /АОД=180-(10+20)=150град., тогда меньший угол равен 180-150=30град.
S=1/2·АС·ВД·Sin30, S=1/2·8·9·1/2=18cм²