Периметр равностороннего треугольника равен 60 см. найти длину средней линии и площадь треугольника. если можно, объяснить решение как можно подробнее!

👇

Ответ:

Damirok21

16.08.2020

тк треугольник равносторонний и у меня 3 одинаковые стороны то 60:3=20 - длина одной стороны средняя линия треугольника равна половине стороны значит она равно 10
теперь нухжно найти высоту . тк треугольник равносторонний то она делит сторону на 2 равные части по 10 см . у нас образуются 2 тругольника в которых одна стороны: 20см, 10 см и одна является высотой данного, мы можем найти ее по теореме пифагора она является катетом X=корень из (20^2-10^2)=корень из 300
S=A*h\2=20*КОРЕНЬ ИЗ 300\2=10*КОРЕНЬ ИЗ 300

4,4(72 оценок)

Открыть все ответы

Ответ:

paninvla2018

16.08.2020

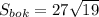
ответ: $S_{bok}=27\sqrt{19}$

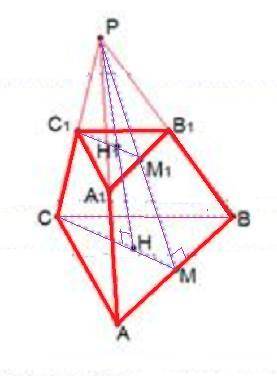
Объяснение: РАВС - правильная треугольная пирамида, АВ=12 , РН=8, А₁В₁С₁║АВС .

АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды. ММ₁ – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости пересекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности

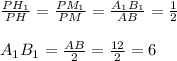
$\frac{PH_1}{PH}=\frac{PM_1}{PM}=\frac{A_1B_1}{AB}=\frac{1}{2}\\\\A_1B_1=\frac{AB}{2}=\frac{12}{2}=6$

Найдём НМ - радиус вписанной окружности в правильный треугольник:

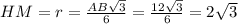
$HM=r=\frac{AB\sqrt3}{6}=\frac{12\sqrt3}{6}=2\sqrt3$

Рассм. ΔРНМ: 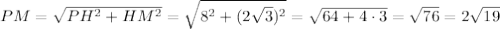$PM=\sqrt{PH^2+HM^2}=\sqrt{8^2+(2\sqrt3)^2}=\sqrt{64+4\cdot 3}=\sqrt{76}=2\sqrt{19}$

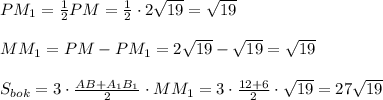
$PM_1=\frac{1}{2}PM=\frac{1}{2}\cdot 2\sqrt{19}=\sqrt{19}\\\\MM_1=PM-PM_1=2\sqrt{19}-\sqrt{19}=\sqrt{19}\\\\S_{bok}=3\cdot \frac{AB+A_1B_1}{2}\cdot MM_1=3\cdot \frac{12+6}{2}\cdot \sqrt{19}=27\sqrt{19}$

Кто-нибудь весь день решаю,не получается

4,7(13 оценок)

Ответ:

dronyuk88

16.08.2020

Угол между образующей конуса и плоскостью основания равен углу между образующей и радиусом основания, проведенного к данной образующей. Площадь боковой поверхности конуса: pi*R*l, площадь основания - pi*R^2. Поскольку площадь боковой поверхности в два раза больше площади основания, то pi*R*l = 2*pi*R^2. упрощаем уравнение: l = 2R. Из рисунка CB = 2OB. Из прямоугольного треугольника COB: угол, который лежит против катета, который в два раза меньше гипотенузы, равен 30 градусов. OB - катет, CB - гипотенуза, следовательно, угол BOC = 30 градусов. Искомый угол CBO = 90 - 30 = 60 градусов.

Площадь боковой поверхности конуса в два раза больше площади основания. найдите угол между образующе