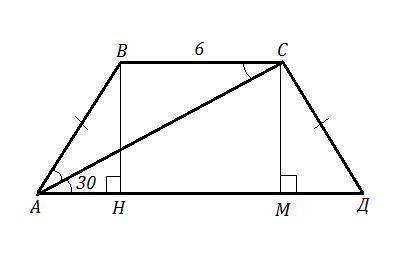
Объяснение:
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.
x+y+2=0,
x-5y+2=0,
5x-y-14=0.
x+y+2=0, x+y+2 = 0
x-5y+2=0|x(-1) -x+5y-2 = 0
6y = 0, y = 0
y = -2-x = -2-0 = -2. Пусть это точка А(-2; 0).
x+y+2=0,
5x-y-14=0.
6х -12 = 0
х = 12/6 = 2,
у = -2-х = -2-2 = -4. Обозначим точку В(2; -4).
x-5y+2=0. x-5y+2 = 0
5x-y-14=0|x(-5) -25x+5y+70 = 0.
-24x + 72 = 0
x = 72/24 = 3.
y = 5x -14 = 5*3-14 = 15-14 =1 это точка С(3; 1).
Расчет длин сторон
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √32 ≈ 5,656854249,
BC = √((Хc-Хв)²+(Ус-Ув)²) = √26 ≈ 5,099019514,
AC = √((Хc-Хa)²+(Ус-Уa)²) = √26 ≈ 5,099019514.
Периметр Р = 15,85489.