Так как точка Р является серединой АВ, а точка Q серединой АС, то РQ – средняя линия треугольника АВС.
Средняя линия параллельна одной из сторон треугольника. Тоесть PQ//BC.
Тогда угол AQP=угол АСВ как соответственные при параллельных прямых PQ u BC и секущей АС;
Угол ВАС – общий;
Тогда ∆АВС~∆APQ по двум углам.
Так как точка Р является серединой АВ, то АР/АВ=1/2, а точка Q серединой АС, то AQ/AC=1/2.
Следовательно: АР/АВ=AQ/AС, тоесть стороны ∆APQ относятся к сторонам ∆АВС в равных отношениях, тоесть стороны одного треугольника пропорциональны сторонам другого;
Угол ВАС – общий;
Тогда ∆АВС~∆APQ по двум пропорциональным сторонам и углу между ними.
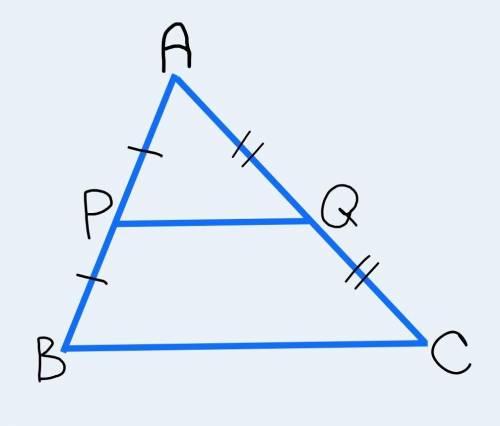
Внимание : тут два варианта .
62 или 58 см
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=11 и =СD (как стороны парал);
2) ВС=11+9=20=АD;
3) Р =( 11+20)*2=62 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=9 и =АВ (как стороны парал);
2) ВС=11+9=26=АD;
3) Р =( 9+20)*2=58
Чертёж в приложении.
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
Даны точки А(7; 6), B(8; 9) и C(3; 7).
Для уравнения окружности нужны координаты её центра и радиус.
Найдём уравнения двух срединных перпендикуляров и точка их пересечения и есть центр описанной окружности.
Вектор АВ = (1; 3), уравнение АВ: (x - 7)/1 = (y - 6)/3 или в общем виде
3x - y - 15 = 0.
Вектор ВC = (-5; -2), уравнение BC: (x - 8)/(-5) = (y - 9)/(-2) или в общем виде 2x - 5y + 29 = 0.
Находим координаты середин сторон АВ и ВС.
С1 = (А+В)/2 = (7,5; 7,5), А1 = (В+С)/2 = (5,5; 8)
Уравнения перпендикуляров через точки (координаты Аи В меняем на -В и А):
С1: x + 3y + C = 0, подставим координаты точки С1:
1*7,5 + 3*7,5 + С = 0, отсюда С = -30, уравнение x + 3y - 30 = 0
A1: 5x + 2y + C = 0, подставим координаты точки А1:
5*5,5 + 2*8 + С = 0, отсюда С = -43,5.
Уравнение 5x + 2y - 43,5 = 0 или с целыми коэффициентами
10x + 4y - 87 = 0.
Находим центр окружности, решая систему:
{x + 3y - 30 = 0,
{10x + 4y - 87 = 0.
Получаем х(О) = 141/26 ≈ 5,42308, у(О) = 639/78 ≈ 8,19231.
Радиус равен 2,700536874 (находим по двум точкам А и О).
ответ: уравнение описанной окружности
(x - (141/26))² + (y - (639/78))² = 2,700536874².