2) Точки Е; М; К; Р – середины соответствующих отрезков АВ; АС; DС и DВ ( DСВА – тетраэдр). Найдите периметр четырёхугольника ЕМКР, если ВС = 8см, АD = 12см.
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
Тогда дм²
––––––––––
2)
По условию
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
№1) Основание прямой призмы -прямоугольный треугольник с гипотенузой 10 см и острым углом 30°. Диагональ боковой грани ,содержащей катет ,противолежащий данному углу ,равна 13 см . Найдите объём призмы. Катет, противолежащий углу 30°, равен половине гипотенузы ВС AB=10:2=5 см Диагональ боковой грани - гипотенуза прямоугольного треугольника с катетами АВ=5 и АА1. Считать не буду, т.к. очевидно, что стороны треугольника АВА1 составляют тройку Пифагора 13,12,5, и , т.к. ВА=5, то высота АА1=12. ( можете по т.Пифагора вычислить с тем же результатом) V=S(ABC)*h S=AB*AC:2 AC= ВС*sin(60°)=5√3 V=12*5√3=60√3 №2) Образующая конуса равна 5 см, а площадь его осевого сечения - 12 см² . Найдите полную поверхность и объём конуса, если его радиус меньше высоты.
Для ответа на вопрос задачи нужно найти радиус и высоту. Осевое сечение конуса - равнобедренный треугольник. Высота конуса делит этот треугольник на 2 прямоугольных, каждый из которых, судя по гипотенузе (образующей конуса) и площади сечения, может быть египетским. Тогда радиус будет 3, высота 4 (радиус меньше высоты по условию) Проверим: Площадь осевого сечения 12, площадь треугольника АВС=6*4:2=12 Следовательно, высота =4, радиус=3. Полная поверхность = площадь боковой поверхности +площадь основания. S полн=πrl+πr² Sполн=π3*5+π9=24π V=πr²h:3=π9*4:3=12π ------------ Если требуется обязательное нахождение радиуса путем вычислений, то с формулы площади треугольника и теоремы Пифагора нужно составить систему уравнений: |hr=12 |h²+r²=25 домножив обе части первого уравнения на 2 и сложив оба уравнения, получим: h²+2hr+r²=25+24 (h+r)²=49 (h+r)=√49 h+r=7 h=7-r h²+r²=25 (7-r)²+r²=25 из получившегося квадратного уравнения 2r²-14r+24=0 корни равны 3 и 4, 3- радиус, 4 -высота конуса. --------------- Подробное решение третьей задачи есть на Сервисе Школьные знания, его нетрудно найти. ---------------- [email protected]
1)
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
Тогда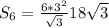 дм²
дм²
––––––––––
2)
По условию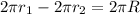
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k=АВ:ВК=7:2 ⇒
S (ABC):S(BKM)=k²= 49/4
245:S(BKM)=49:4⇒
S(Δ BKM)=20
S(ТКМОНР)=245-3•20=185 мм²