Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их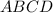 
и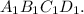 
Проведём диагональ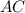 
в квадрате 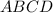и диагональ 
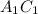в квадрате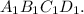
Рассмотрим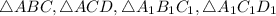 
.
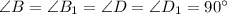, по свойству квадрата.
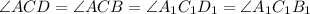, так как диагонали квадрата делят углы пополам.
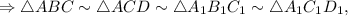по 1 признаку подобия треугольников.
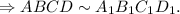
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.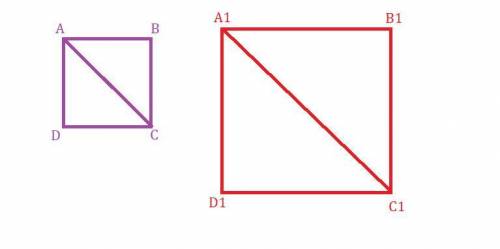
кратное 18 ---> оно делится на 2 и на 9
т.е. оно четное --- заканчивается на 0 или 2 или 4 или 6 или 8
и сумма цифр числа делится на 9 (это признак делимости на 9)))
получим варианты:
a b с d 0
a b с d 2
a b с d 4
a b с d 6
a b с d 8
и теперь второе условие: соседние цифры отличаются на 2
для первого варианта: a b с 2 0, a b 0 2 0 или a b 4 2 0
a+b+2 = 9 или a+b+4+2 = 9
a+b = 7 a+b = 3 ---> 12420, например
18 * 690 = 12420
но, первые цифры не на 2 отличаются... не получилось...
но смысл рассуждений такой же)))
пробуем еще...
у меня получилось:
24246 / 18 = 1347
можно попробовать и еще найти...