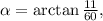Question

1)диагонали ромба равны 6см и 8см. найдите его углы 2) . найдите неизвестные стороны и углы прямоугольного треугольника, если его катеты равны 11см и 60см.

Answer 1

Задачи стоят дороже

1) Найти можно половинку углов. Рассмотрим треугольники, которые получаются при пересечении диагоналей. Их четыре. Рассмотрим любой из них. Этот треугольник прямоугольный. Так как по свойства ромба, его диагонали пересекаются под прямым углом и делятся пополам. одна сторона равна 3 см, вторая 4 см. Значит гипотенуза равна

$\sqrt{3^2+4^2}=5$

Угол, противолежащий катету в 3 см можно выразить через тангенс (отношение противолежащего катета у прилежащему)

$\tan\beta=\frac{3}{4}.$

Угол, противолежащий катету в 4 см тоже можно выразить через тангенс

$\tan\alpha=\frac{4}{3}.$

Заметим, что это лишь половины углов ромба, так как диагонали ромба делят пополам углы ромба. 

Значит по формуле двойного угла для тангенсов

$\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}$

$\tan2\alpha=\frac{2*\frac{4}{3}}{1-\left(\frac{4}{3}\right)^2}$

$\tan2\alpha=\frac{\frac{8}{3}}{1-\frac{16}{9}}$

$\tan2\alpha=\frac{\frac{8}{3}}{\frac{-7}{9}}$

$\tan2\alpha=-\frac{24}{7}$

Значит угол равен

$2\alpha=\arctan\frac{-24}{7}$ - это первый угол.

Второй угол равен

$\tan2\beta=\frac{2\tan\beta}{1-\tan^2\beta}$

$\tan2\beta=\frac{2\frac{3}{4}}{1-\left(\frac{3}{4})\right^2}$

$\tan2\beta=\frac{\frac{3}{2}}{1-\frac{9}{16}}$

$\tan2\beta=\frac{\frac{3}{2}}{\frac{7}{16}}$

$\tan2\beta=\frac{24}{7}$

Второй угол равен

$2\beta=\arctan\left(\frac{24}{7}\right)$

ответ: углы ромба равны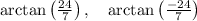 $\arctan\left(\frac{24}{7}\right),\quad \arctan\left(\frac{-24}{7}\right)$

2) Гипотенузу найти легко по теореме Пифагора

$\sqrt{11^2+60^2}=\sqrt{121+3600}=\sqrt{3721}=61$

Углы чуть сложнее. Воспользуемся опять тангенсом.

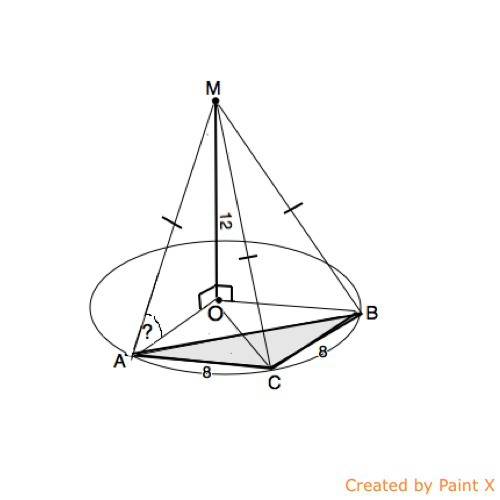
Угол напротив стороны в 11 см равен

$\alpha=\arctan\frac{11}{60}$

Угол напротив стороны в 60 см равен

$\beta=\arctan\frac{60}{11}$

ответ: 61 см гипотенуза, $\alpha=\arctan\frac{11}{60},$

$\beta=\arctan\frac{60}{11}$