
или
15° и 75°
Объяснение:
Обозначим в прямоугольном треугольнике
катеты как a, b
гипотенузу как с (с = 4)
и углы как 
Причем углы связаны формулой

Тогда площадь треугольника, равная 2, равна половине произведения катетов:
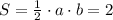
Однако для острого угла в прямоугольном треугольнике отношение прилежащего катета к гипотенузе - это косинус угла, а отношение противолежащего катета к гипотенузе - это синус угла
Соответственно, каждый из катетов можно выразить через синус и косинус одного из острых углов:
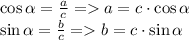
Т.к. с = 4, получаем:

Получаем ригонометрическое уравнение:

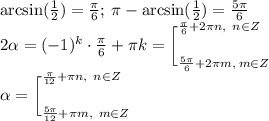
Т.к. мы ищем углы в прямоугольном треугольнике, то

Соответственно попадают в этот интервал только следующие полученные углы:


Итак, мы получили 2 пары углов:

Очевидно, что это одна и та же пара углов, в зависимости от того, какой катет мы брали за а, а какой за b.
Итак, получаем ответ:

Поскольку в условии задачи не указано, лежат ли прямые в одной плоскости или нет, то они необязательно параллельны.
В планиметрии две прямые могут быть параллельными или пересекаться.
Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.
Если две прямые лежат в одной плоскости и не пересекаются, то они - параллельны.
. В стереометрии две прямые могут не пересекаться, но в то же время не быть параллельными.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Скрещивающиеся прямые лежат в параллельных плоскостях, но плоскость провести через них, как это можно сделать через две параллельные прямые, невозможно
Рассмотрим это на ребрах куба (см. приложение)