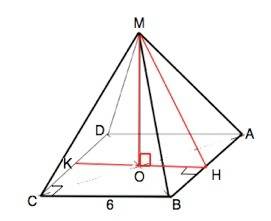
Обозначим пирамиду МАВСD. В её основании - квадрат.
В правильной пирамиде высота проходит через центр основания. Для квадрата это точка пересечения диагоналей. МО – высота пирамиды, МН –апофема.
Формула площади квадрата:
S=a²⇒ а=√36=6 см - сторона основания
Площадь боковой поверхности равна сумме площадей боковых граней, которые в правильной пирамиде - равнобедренные треугольники и равны.
Площадь одной грани равна 48²4=12 см²
Площадь Δ АМВ=S=a•h:2 --
h=12:3=4 см
Проведем через основание МО параллельно СВ прямую КН=СВ=6 см
ОН=КН:2=3 см
Из прямоугольного ∆ МОН высота МО=√(MH²-OH²)=√(16-9)=√7
Условие не совсем понятное:
если прямоугольный треугольник лежит в основании призмы,то
V=S(основания)*H=1\2*8*6*10=240
если в основании пирамиды то V=1\3*H*S=1\3*240=80