13 Read and correct the mistakes. 200 1 Trains in Kazakhstan can travel up to 20 kilometres an hour 2 You can find husky sleds in Thailand. 3 Husky sleds can travel over water. 4 Cable cars in Brazil carry 120 people every day. 5 Tuk-tuks are four-wheeled taxis. 6 Tuk-tuks haven't got any wheels
Нужно найти отрезок PO. Для этого нужно найти треугольник, из которого можно посчитать PO по теореме Пифагора( то есть прямоугольный треугольник, в котором участвует PO). Раз такого треугольника не видим явно из условия, придется его построить, при этом нужно задействовать известные данные. Нам известна диагональ квадрата, значит, можно посчитать его сторону, также известна длина отрезка PH.
Поэтому построим треугольник POH, проведем OH. Треугольник POH будет прямоугольным, потому что PO - отрезок, соединяющий вершину правильной пирамиды с центром ее основания, а такой отрезок перпендикулярен основанию пирамиды. Тогда в ΔPOH угол ∠POH - прямой.
Осталось найти OH. Так как PO перпендикулярно плоскости основания, а PH перпендикулярно BC, то по следствию из теоремы о трех перпендикулярах OH будет перпендикулярно BC.
H - середина BC(PH - высота равнобедренного треугольника, значит, PH также и медиана, а Δ-к равнобедренный, потому что пирамида правильная ), поэтому CH в 2 раза меньше BC. Прямоугольные треугольники OHC и ABC подобны по двум углам, поэтому OH также в 2 раза меньше AB.
AB - сторона квадрата ABCD, а сторона квадрата в меньше его диагонали. Тогда AB = 12/
Высота трапеции равна диаметру вписанной окружности: ВН = СК = 7,5 · 2 = 15 см ΔАВН: ∠АНВ = 90°, по теореме Пифагора АН = √(АВ² - ВН²) = √(17² - 15²) = √(289 - 225) = √64 = 8 см ΔАВН = ΔDCK по катету и гипотенузе (АВ = CD по условию, ВН = СК как высоты трапеции), ⇒ DK = AH = 8 см
Если в четырехугольник вписана окружность, то суммы противоположных сторон равны: AD + BC = AB + CD = 17 + 17 = 34 см AD = AH + HK + KD = 8 + HK + 8 = HK + 16 Так как НК = ВС: AD + BC = 34 AD = BC + 16
2BC + 16 = 34 BC = (34 - 16)/2 = 18/2 = 9 см AD = 9 + 16 = 25 см
Объяснение:
5. Нарисуем пирамиду, назовем центр основания O.
Нужно найти отрезок PO. Для этого нужно найти треугольник, из которого можно посчитать PO по теореме Пифагора( то есть прямоугольный треугольник, в котором участвует PO). Раз такого треугольника не видим явно из условия, придется его построить, при этом нужно задействовать известные данные. Нам известна диагональ квадрата, значит, можно посчитать его сторону, также известна длина отрезка PH.
Поэтому построим треугольник POH, проведем OH. Треугольник POH будет прямоугольным, потому что PO - отрезок, соединяющий вершину правильной пирамиды с центром ее основания, а такой отрезок перпендикулярен основанию пирамиды. Тогда в ΔPOH угол ∠POH - прямой.
Осталось найти OH. Так как PO перпендикулярно плоскости основания, а PH перпендикулярно BC, то по следствию из теоремы о трех перпендикулярах OH будет перпендикулярно BC.
H - середина BC(PH - высота равнобедренного треугольника, значит, PH также и медиана, а Δ-к равнобедренный, потому что пирамида правильная ), поэтому CH в 2 раза меньше BC. Прямоугольные треугольники OHC и ABC подобны по двум углам, поэтому OH также в 2 раза меньше AB.
AB - сторона квадрата ABCD, а сторона квадрата в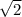
меньше его диагонали. Тогда AB = 12/
Теперь находим OP по теореме Пифагора
OP =
= 
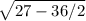= 3 см