Даны точки A (– 1; 3), B (1; 5), C (3; 3), D (1; 1).
Если не известно, какая фигура заданный четырёхугольник, то проще его разделить на 2 треугольника: АВС и АСД. Найти их площади и сложить.
Вектор a (АВ) Вектор b (АС)
x y x y
2 2 4 0
4 4 16 0 Квадраты
8 16 Сумма квадратов
Модуль =√8=2√2 ≈ 2,8284 4
Скалярное произведение ABxAC = (2*4 + 2*0) = 8.
cos ВAС = 0,707106781
Угол ВAС = 0,7854 радиан
45 градусов.
Вектор e (АD)
x y
2 -2
4 4
8
2,828427125
Скалярное произведение AСxAD = 8
cos CAD= 0,707106781
Угол CAD = 0,7854 радиан
45 градусов.
S(ABCD) = (1/2)*(AB*AC*sinA+AC*AD*sinCAD)
S(ABCD) = 0,5 *(8+8) = 8.
НАСТЯ ПРИВЕТ
Объяснение:
у прямокутнику abcd на діагоналі ac вибрана така точка k для якої cb=ck на стороні bc вибрана така точка m для якої km=mc, доведіть що ak+bm+cmу прямокутнику abcd на діагоналі ac вибрана така точка k для якої cb=ck на стороні bc вибрана така точка m для якої km=mc, доведіть що ak+bm+cmу прямокутнику abcd на діагоналі ac вибрана така точка k для якої cb=ck на стороні bc вибрана така точка m для якої km=mc, доведіть що ak+bm+cmу прямокутнику abcd на діагоналі ac вибрана така точка k для якої cb=ck на стороні bc вибрана така точка m для якої km=mc, доведіть що ak+bm+cm
По формуле двойного угла
sin(2a)=2*sina*cosa
Известно, что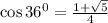
Во втором примере воспользуемся формулой
Вычислим отдельно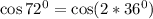
По формуле двойного угла для косинуса
Значит
Вернемся к (2)