
1. 60
2. АВ = 70°, АС = ВС = 145°.
Объяснение:
1.
Дано:
Окружность (О; r)
∠OBA = 30°
CA — касательная
Найти:
∠BAC — ?
1) Так как радиусы окружности равны, значит, две стороны треугольника ABO равны. ⇒ ΔABO равнобедренный (AO = OB).
У равнобедренного треугольника углы при основании равны, следовательно: ∠OBA = ∠OAB = 30°.
2) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания, значит CA ⊥ OA. ∠OAC = 90°.
3) ∠BAC = ∠OAC - ∠OAB.
∠BAC = 90° - 30° = 60°.
2 Задача
Если О - центр окружности, то угол АОВ - центральный.
Центральный угол равен дуге, на которую опирается. Отсюда, дуга АВ = 70°.
Угол САВ = углу СВА, тогда дуга АС = дуге ВС = (360° - 70°) / 2 = 290° / 2 = 145°.
Смотри рисунок.
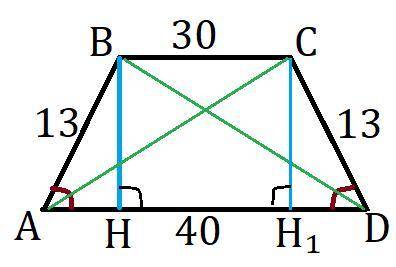
Диагонали равны т.к. углы при при основании и боковые стороны равнобокой трапеции равны (ΔABD=ΔACD). Из вершины B проведём высоты BH на сторону AD и высоту CH₁. BH=CH₁ как расстояние между параллельными прямыми, AB=CD как боковые стороны равнобокой трапеции и ∠CDH₁=∠BAH как углы при основании этой трапеции получается что ΔCDH₁=ΔBAH по катету, гипотенузе и углу. Таким образом AH=DH₁ как соответственные стороны равных треугольников.
BCH₁H это прямоугольник т.к. противоположные стороны параллельны и равны, а угол между ними 90°, то есть BC=HH₁. Найдём AH:
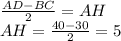
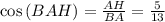 как угол я прямоугольном треугольнике. Тогда по теореме косинусов можно найти BD:
как угол я прямоугольном треугольнике. Тогда по теореме косинусов можно найти BD:
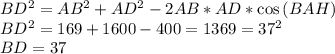
ответ: 37дм
Размерности были везде одинаковыми, поэтому можно было их и не писать.
32°.
. .. . ..
Объяснение:
360-328=32°.