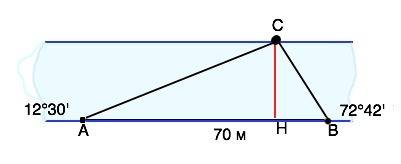
Ширина реки равна длине расстояния СН, измеренного перпендикулярно между ее берегами, иначе - высоте СН треугольника АВС. .
Алгоритм решения:
а) По т.синусов вычислим АС,
б) вычислим площадь ∆ АВС.
в) из площади найдем высоту СН, равную ширине реки.
—————
а ) Угол С=180°- (угол А+угол В)
угол А=12°30’=12,5°
B=72°42’=72,8°
Угол С=180°-(12,5°+72,8°=94,8°
АВ:sin 72,8=AC:sn 94,8°
sin 72,8=0.95476
sin94,8°=0.99649 , откуда АВ=67.0684
б) S (ABC)=AC•AB•sin(CAB):2
S (ABC)=508
CH=2S:AC=1016:70=14,5 м
L: 2y=3x-4 или у=(3/2)х-2
Уравнение параллельной ей прямой имеет вид
у=(3/2)х+b
Чтобы найти b подставим координаты точки M в последнее уравнение
0=(3/2)·(-2)+b ⇒ b=3
ответ. Уравнение прямой . параллельной 3x-2y-4=0 и проходящей через точку M имеет вид
у=(3/2)х+3 или 2у-3х-6=0
2)Если прямые у= k₁x+b₁ и y=k₂x+b₂ взаимно перпендикулярны, то k₁·k₂=-1
Уравнение прямой, перпендикулярной прямой L имеет вид
у= (- 2/3)х+ c
Чтобы найти c подставим координаты точки M в последнее уравнение
0=(-2/3)·(-2)+b ⇒ b=-4/3
ответ. Уравнение прямой . перпендикулярной прямой 3x-2y-4=0 и проходящей через точку M имеет вид
у=(-2/3)х-4/3 или 3у+2х+4=0
3)Уравнение прямой, проходящей под углом 45 ° к прямой L имеет угловой коэффициент
k=(3/2+1)/(1-3/2)=2,5:(-0,5)=-5
Для нахождения применили геометрический смысл коэффициента k k=tgα
Искомая прямая составляет с осью ох угол (α+45 °)
tg(α+45 °)= (tg α+ tg 45 °)/(1-tg αtg 45 °)=(3/2+1)/(1-3/2)=2,5:(-0,5)=-5
y=-5х+d
Чтобы найти d подставим координаты точки M в последнее уравнение
0=(-5)·(-2)+d ⇒ d=-10
ответ. Уравнение прямой . составляющей с прямой 3x-2y-4=0 угол в 45° и проходящей через точку M имеет вид
у=-5х-10 или у+5х+10=0
Для построения прямой достаточно двух точек
Прямая L проходит через точки х = 0, y = - 2
x = 4, y = 4
Прямая 2y-3x-6=0 проходит через точки
х = 0 , y = 3
x = - 2, y = 0
Прямая 3y+2x+4=0 проходит через точки
х =4 , y = - 4
x =- 2, y = 0
Прямая у+5х+10=0 проходит через точки
х = 0 , y = - 10
x = - 2, y = 0