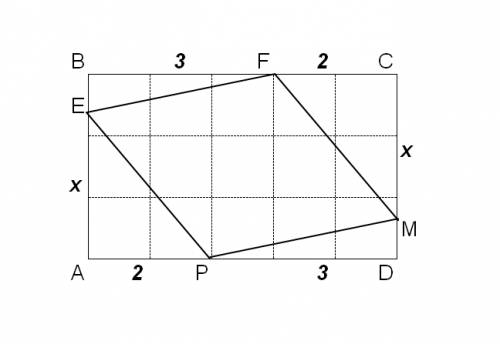
Из соображений симметрии FC=AP=2 и AE=CM=x (неизвестная длина)
Ромб - четырехугольник, у которого все стороны равны:
PE=EF=FM=MP (гипотенузы треугольников PAE, EBF, FCM, MDP)
По теореме Пифагора
2^2+x^2=(3-x)^2+3^2
4+x^2=9-6x+x^2+9
6x=14
x=7/3
Нашли все отрезки:
AE=CM=7/3
EB=MD=2/3
Далее находим сумму площадей всех треугольников PAE, EBF, FCM, MDP
St=(1/2)*2*(7/3)+(1/2)*3*(2/3)+(1/2)*2*(7/3)+(1/2)*3*(2/3)=7/3+1+7/3+1=20/3
Площадь прямоугольника S=5*3=15
Площадь ромба s=S-St=15-20/3=25/3
Отношение площадей прямоугольника и ромба
S/s=15/(25/3)=9/5
ответ: отношение площадей прямоугольника и ромба = 9/5
Приклад 1. З вершини квадрата АВСD проведено перпендикуляр АК до площини квадрата. Знайти площу квадрата, якщо КD = 5 см; КС = 13 см.Розв’язання (мал. 416). 1) АК АВС; КD - похила; АDБ - її проекція. Оскільки АD DС, то за теоремою про три перпендикуляри маємо КD DС.3) Тоді площа квадрата S = 82 = 64 (см2).
Приклад 2. Сторони трикутника довжиною 4 см, 13 см і 15 см. Через вершину найбільшого кута до площини трикутника проведено перпендикуляр і з його кінця, що не належить трикутнику, проведено перпендикуляр завдовжки 4 см до протилежної сторони цього кута. Знайти довжину перпендикуляра, проведеного до площини трикутника.Розв’язання. 1) У ∆АВС: АВ = 4 см; ВС = 13 см; АС = 15 см. Оскільки АС - найбільша сторона трикутника, то АВС - найбільший кут трикутника. ВК АВС (мал. 417).2) КМ АС, тоді за теоремою про три перпендикуляри: ВМ АС, тобто ВМ - висота ∆АВС. За умовою: КМ = 4см.3) Знайдемо площу трикутника АВС за формулою Герона.4) 3 іншого боку