ответ: 12 (ед. длины)
Объяснение:
Одна из формул биссектрисы треугольника
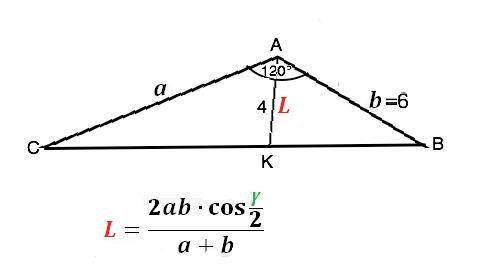
L={2ab•cos(0,5γ)}:(a+b) ,
где L биссектриса, а и b- стороны, γ - угол между ними.
На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6, угол А=γ =120°
cos0,5γ=cos60°=1/2
4=2a•6•0,5/(a+6) =>
4a+24=6a =>
АС=a=12 (ед. длины)
Или с тем же результатом найти:
1) По т. косинусов из ∆ АКВ найти КВ
2) по т. синусов из ∆ АКВ угол В
3) из суммы углов треугольника угол С
4) по т. синусов вычислить длину искомой стороны АС
1)Если периметр 12 см, то длина каждой стороны будет (12/4)=3 мм.
Тупой угол 120 гр. Тогда острый=60 градусов. Диагональ ромба делит угол пополам. Значит, получим 4 равных треугольника с острым углом 30 гр. А катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Таким образом, катет будет (3/2)=1,5 мм. Второй катет по т.Пифагора можно найти.
Теперь легко вычислить площадь прямоугольного треугольника (S=1/2*a*b), а площадь ромба будет равна 4 площадям треугольника.
Дерзайте с вычислениями!
Дано и нужно найти - это Вы умеете и обязательно сможете написать сами.
Нет, не может. Он должен быть больше 6 см.
Доказательство 1)
Соединим точку В с А и О.
Получим треугольник АОВ со стороной АО=13 см, АВ =4 см, ОВ< 6 cм, так как точка В находится внутри окружности и потому меньше ее радиуса.
Сумма длин двух сторон треугольника больше длины третьей стороны, иначе эти стороны не образуют угол просто потому, что не смогут соединиться.
При АВ=4
АВ+ВО < 13 см
Доказательство 2)
Проведем касательную к точке С пересечения АО с окружностью. Любой отрезок, пересекающий эту касательную по обе стороны от точки М, будет длиннее АС, так как он будет наклонным к касательной. А, как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой.
В данном случае АС будет больше АВ. Длина же АС=13-6=7 см.
АВ >7 см