Добрый день) Не знаю правильно ли моё решение. Но вот.. во вложениях файл. Поправьте если что)

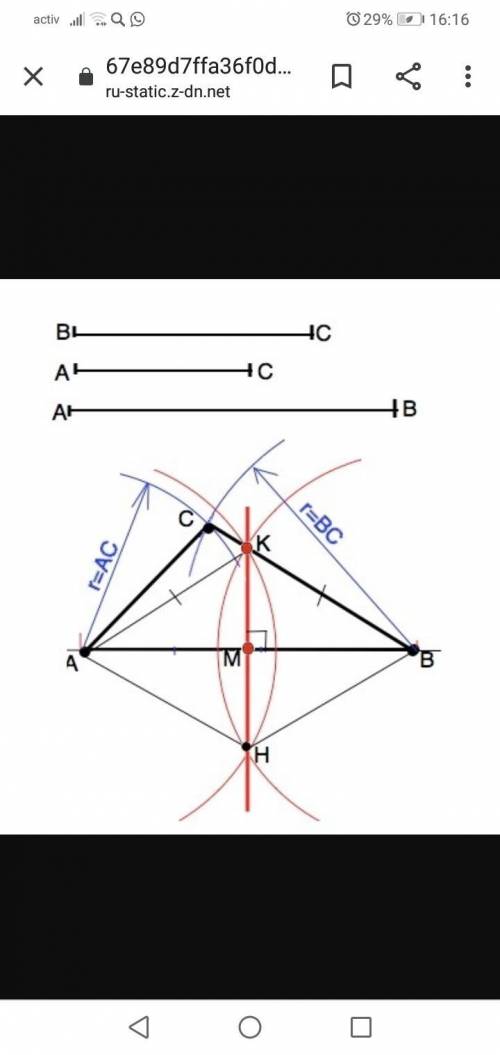
ответ:. На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг - вершина С искомого треугольника.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса, но больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
Объяснение: делал на скорую руку
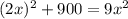
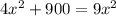
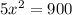
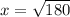
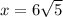 , то есть на одну часть приходится
, то есть на одну часть приходится 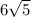 см.
см. 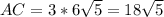 см
см 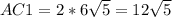 см
см 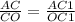
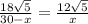
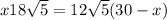
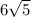 :
: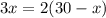
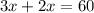

как усложняют понимание условия ненужные подробности. Причем условие дано не точно.
Решаю такую задачу.
Нужно найти радиус окружности, вписанной в равнобедренный треугольник с основанием 6 и углом при основании Ф, sin(Ф) = 4/5.
Сразу ясно, что MNB составлен из двух египетских треугольников (3,4,5), то есть высота треугольника MNB 4, боковые стороны 5.
Отсюда площадь 12, периметр 16, радиус вписанной окружности 2*12/16 = 3/2.