Вершины вписанного квадрата лежат на описанной около него окружности. Диагональ квадрата - диаметр этой окружности.
Диагональ вписанного квадрата со стороной 8 см по теореме Пифагора DC=√(DH²+CH²) или DC=СН:sin45°=8√2, ⇒ радиус ОН =D:2=4√2 см. (См. рисунок). Соединим вершины А и В шестиугольника с центром О вписанной в него окружности.
Центральный угол АОВ=360°:6=60°, треугольник АОВ - равносторонний. Радиус вписанной окружности является его высотой. сторона АВ=АО=ОН:sin60°=(4√2):√3/2=(8√2):√3 или см
Луч- прямая, которая имеет начало, но не имеет конца.
Угол- часть плоскости между двумя линиями, исходящими из одной точки.
Треугольник- Геометрическая фигура, образованная тремя пересекающимися прямыми, образующими три внутренних угла, а также всякий предмет, устройство такой формы.
Прямоугольник- Прямоугольником называется параллелограмм, у которого все углы прямые.
Круг- Часть плоскости, ограниченная окружностью, а также сама окружность.
Шар- Геометрическое тело, образованное вращением круга вокруг своего диаметра
Цилиндр- геометрическое тело, образуемое вращением прямоугольника вокруг одной из его сторон.
Вершины вписанного квадрата лежат на описанной около него окружности. Диагональ квадрата - диаметр этой окружности.
Диагональ вписанного квадрата со стороной 8 см по теореме Пифагора DC=√(DH²+CH²) или DC=СН:sin45°=8√2, ⇒ радиус ОН =D:2=4√2 см. (См. рисунок). Соединим вершины А и В шестиугольника с центром О вписанной в него окружности.
Центральный угол АОВ=360°:6=60°, треугольник АОВ - равносторонний. Радиус вписанной окружности является его высотой. сторона АВ=АО=ОН:sin60°=(4√2):√3/2=(8√2):√3 или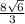 см
см